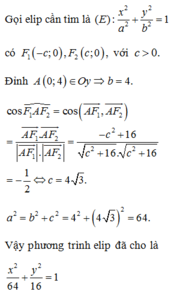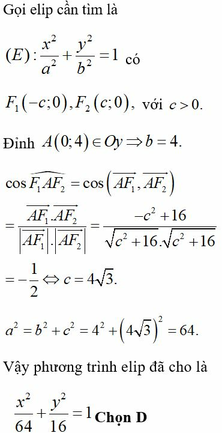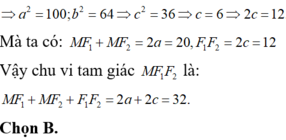36. Cho elip có các tiêu điểm F1(-5;0) , F2(5;0) và 1 điểm M thuộc elip sao cho chu vi dentaMF1F2=30. Tìm pt chính tăc của elip.
Những câu hỏi liên quan
Cho elip (E) có các tiêu điểm
F
1
-
5
;
0
,
F
2
5
;
0
và một điểm M nằm trên (E) sao cho chu vi của tam giác
M
F
1
F
2
bằng 30. Khi đó phương trình chính tắc của elip là: A. ...
Đọc tiếp
Cho elip (E) có các tiêu điểm F 1 - 5 ; 0 , F 2 5 ; 0 và một điểm M nằm trên (E) sao cho chu vi của tam giác M F 1 F 2 bằng 30. Khi đó phương trình chính tắc của elip là:
A. x 2 75 + y 2 100 = 1
B. 100 x 2 + 75 y 2 = 1
C. 75 x 2 + 100 y 2 = 1
D. x 2 100 + y 2 75 = 1
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là: A.
x
2
25
+
y
2
16
1.
B.
x
2
5
+
y
2
4
1.
C. ...
Đọc tiếp
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:
A. x 2 25 + y 2 16 = 1.
B. x 2 5 + y 2 4 = 1.
C. x 2 25 + y 2 9 = 1.
D. x 5 + y 4 = 1.
Cho Elip có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của elip.
Ta có: \({a^2} = 36,{b^2} = 9 \Rightarrow c = \sqrt {36 - 9} = 3\sqrt 3 \) nên elip có hai tiêu điểm là \({F_1}\left( { - 3\sqrt 3 ;0} \right);{F_2}\left( {3\sqrt 3 ;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\sqrt 3 \).
Đúng 0
Bình luận (0)
Cho elip có phương trình
x
2
52
+
y
2
36
1
Với M bất kì thuộc elip thì diện tích lớn nhất của tam giác MF1F2 (F1, F2 là tiêu điểm của elip) là A. 24 B. 48 C. 288 D. 144
Đọc tiếp
Cho elip có phương trình x 2 52 + y 2 36 = 1 Với M bất kì thuộc elip thì diện tích lớn nhất của tam giác MF1F2 (F1, F2 là tiêu điểm của elip) là
A. 24
B. 48
C. 288
D. 144
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là
F
1
-
3
;
0
và điểm
M
1
;
3
2
nằm trên elip...
Đọc tiếp
Lập phương trình chính tắc của elip trong trường hợp sau: Elip có một tiêu điểm là F 1 - 3 ; 0 và điểm M 1 ; 3 2 nằm trên elip.
Gọi Elip cần tìm có dạng : (E) :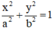 
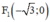là tiêu điểm của (E) ⇒ a2 – b2 = 3 ⇒ a2 = b2 + 3
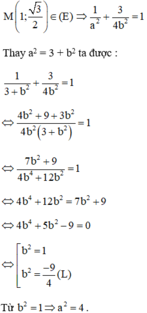
Phương trình chính tắc của Elip là :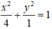 
Đúng 1
Bình luận (0)
cho elip (e) có pt chính tắc: x^2/9 + y^2/4=1
a) tìm tọa độ đỉnh, tiêu điểm f1, f2, và tâm sai của (e)
b) tìm tọa độ điểm m thuộc (e) thõa mãn mf1 -mf2=2
(f1 là tiêu điểm bên trái của elip)
Cho elip
E
:
x
2
25
+
y
2
9
1
có hai tiêu điểm
F
1
;
F
2
. Hai điểm M, N phân biệt thuộc elip
E
thỏa mãn
M
F
1
+
N...
Đọc tiếp
Cho elip E : x 2 25 + y 2 9 = 1 có hai tiêu điểm F 1 ; F 2 . Hai điểm M, N phân biệt thuộc elip E thỏa mãn M F 1 + N F 2 = 14 . Tính giá trị của biểu thức M F 2 + N F 1
A. M F 2 + N F 1 = 2
B. M F 2 + N F 1 = 4
C. M F 2 + N F 1 = 8
D. M F 2 + N F 1 = 6
Chọn đáp án D
MEMORIZE |
Định nghĩa đường elip, phương trình chính tắc của elip. |
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
°
. Phương trình chính tắc của elip đã cho là
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ° . Phương trình chính tắc của elip đã cho là
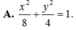
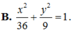
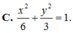
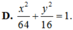
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm
F
1
,
F
2
dưới một góc bằng
120
∘
. Phương trình chính tắc của elip đã cho là A.
x
2
8
+
y
2
4
1
B.
x...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho elip có đỉnh A(0;4) nhìn hai tiêu điểm F 1 , F 2 dưới một góc bằng 120 ∘ . Phương trình chính tắc của elip đã cho là
A. x 2 8 + y 2 4 = 1
B. x 2 36 + y 2 9 = 1
C. x 2 6 + y 2 3 = 1
D. x 2 64 + y 2 16 = 1
Cho elip có phương trình
x
2
100
+
y
2
64
1
Với hai tiêu điểm F1 và F2 với một điể M bất kì nằm trên elip thì chu vi tam giác MF1F2 là A. 16 B. 32 C. 36 D. 72
Đọc tiếp
Cho elip có phương trình x 2 100 + y 2 64 = 1 Với hai tiêu điểm F1 và F2 với một điể M bất kì nằm trên elip thì chu vi tam giác MF1F2 là
A. 16
B. 32
C. 36
D. 72
