Tam giác ABC có H(-7;-1) là chân đường cao hạ từ A xuống BC. I(-4;-4) là tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ ABC biết phân giác trong A là d: x + 3y + 11 = 0

Những câu hỏi liên quan
Tam giác ABC có góc B = 45 độ,BC = 7 cm,AB= căn bậc 18 cm.kẻ AH vuông góc với BC,H thuộc BC.tính chu vi tam giác ABC
Ta có: ΔAHB vuông tại H
mà \(\widehat{B}=45^0\)
nên ΔAHB vuông cân tại H
=>AH=HB
Ta có: ΔAHB vuông tại H
nên \(AH^2+HB^2=AB^2\)
=>AH=HB=3cm
=>HC=4cm
=>AC=5cm
C=AB+BC+AC
\(=7+5+3\sqrt{2}=12+3\sqrt{2}\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có BC = 7, ∠ (ABC) = 42 ° , ∠ (ACB) = 35 ° . Gọi H là chân đường cao của tam giác ABC kẻ từ A. Hãy tính AH (làm tròn kết quả đến chữ số thập phân thứ ba).
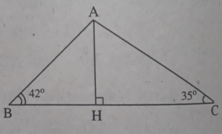
Đặt AH = h thì rõ ràng BH = h.cotg (ABH) = h. cotg 42 °
CH = h.cotg (ACH) = h.cotg 35 ° (để ý rằng H thuộc đoạn BC vì 35 ° , 42 ° đều là góc nhọn).
Do đó: 7 = BC = BH + CH = h(cotg 42 ° + cotg 35 ° ), suy ra
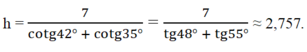
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B=60 độ, AB=7 cm, BC=15 cm. Vẽ AH vuông góc với BC( H thuộc BC). Lấy điểm M trên HC sao cho HM=MB.CM:a. So sánh góc BAC và ACB
b,tam giác ABM đều
c, tam giác ABC có phải tam giác vuông ko? Vì sao?
Bài 7: Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường phân giác BE (E thuộc AC). Kẻ EH vuông góc với BC (H thuộc BC). Gọi K là giao điểm của AB và HE
a) Tính độ dài đoạn thẳng BC
b) Chứng minh rằng: Tam giác ABE= tam giác HBE
c) EK=EC
Các bạn vẽ hình rồi giải nha
a: BC=5cm
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: EK=EC
Đúng 3
Bình luận (0)
Cho tam giác ABC có góc A=80o H là trực tâm tam giác ABC. Gọi M đối xứng với H qua BC.
a) Chứng minh tam giác BHC= tam giác BMC
b) Tính góc BMC
a: Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(BC=7;\widehat{ABC}=42^0;\widehat{ACB}=35^0\). Gọi H là chân đường cao của tam giác ABC kẻ từ A. Hãy tính AH (làm tròn kết quả đến chữ số thập phân thứ ba)
Cho tam giác ABC;B=60 độ ,AB=7 cm,BC=15cm.Tren cạnh BC lấy điểm D sao cho góc BAD=60 độ.Gọi H là trung điểm của BD.
a/Tính độ dài HD
b/Tính độ dài AC
c/Tam giác ABC có phải tam giác vuông không?
Cho tam giác ABC. Vẽ trực tâm H của tam giác ABC và nhận xét vị trí của nó trong các trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
a)

Nhận xét: H là một điểm nằm trong tam giác ABC.
b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.
c)
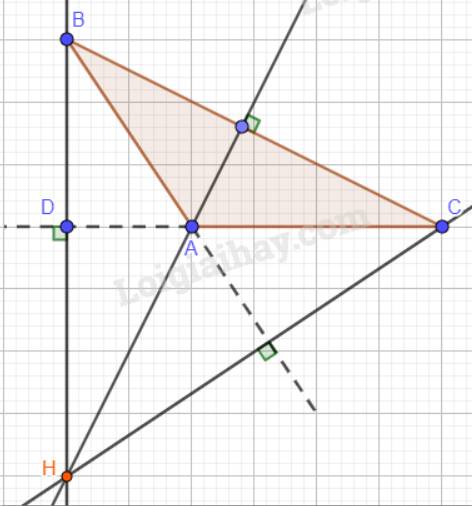
Nhận xét: H nằm ngoài tam giác ABC.
Đúng 0
Bình luận (0)
Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.
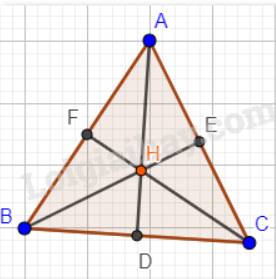
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.
Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD;
\(AD \bot BC; BE \bot AC; CF \bot AB\)
Xét tam giác ADB và tam giác ADC có:
AD chung
\(\widehat{ADB}=\widehat{ADC} (=90^0)\)
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).
Tương tự, ta cũng được, AC = BC
Xét tam giác ABC có AB = AC = BC nên là tam giác đều.
Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, trực tâm H của tam giác chia đường cao AE theo tỉ số 7:1. Giao điểm I của các đường phân giác của tam giác ABC chia AE theo tỉ số nào?



















