Trong mặt phẳng Oxy, cho điểm \(A\left(8;-1\right)\) và đường tròn (C) : \(x^2+y^2-6x-4y+4=0\)
a) Viết phương trình các tiếp tuyến (C) vẽ từ A
b) Gọi M và N là các tiếp điểm của các tiếp tuyến trên với (C). Tính độ dài đoạn MN
Trong mặt phẳng Oxy, cho ba điểm \(D\left( { - 1;4} \right),E\left( {0; - 3} \right),F\left( {5;0} \right)\)
a) Vẽ các điểm D, E, F trên mặt phẳng Oxy
b) Tìm tọa độ của các vectơ \(\overrightarrow {OD} ,\overrightarrow {OE} ,\overrightarrow {OF} \).
c) Vẽ và tìm tọa độ hai vectơ đơn vị và \(\overrightarrow j \)lần lượt trên hai trục tọa độ Ox và Oy
a)
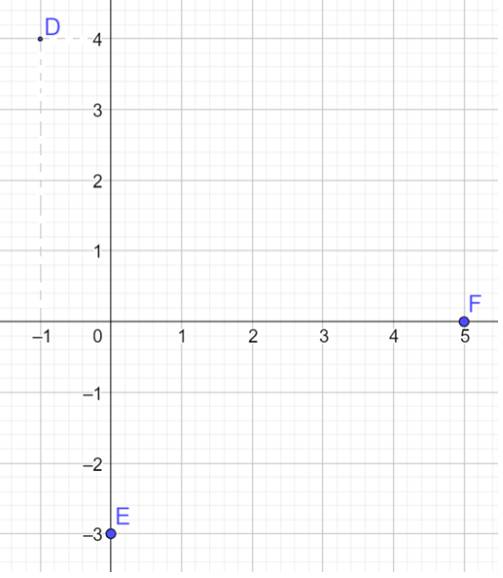
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
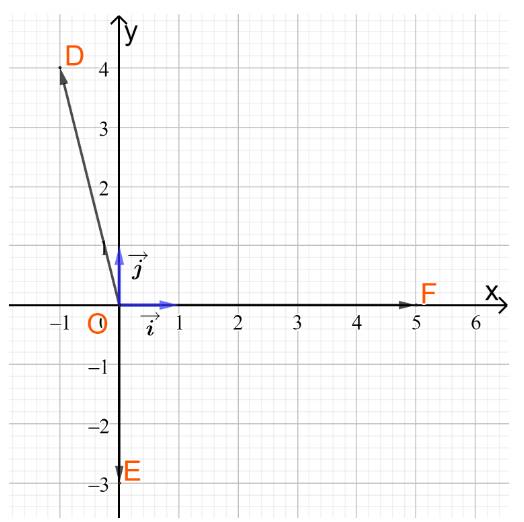
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)
(1) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(1;-4\right)\), \(\overrightarrow{b}=\left(0;2\right)\). tọa độ của vecto \(\overrightarrow{u}=2\overrightarrow{a}-\overrightarrow{b}\) là?
(2) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(-7;3\right)\), \(\overrightarrow{b}=\left(4;1\right)\). tọa độ của vecto \(\overrightarrow{u}=\overrightarrow{b}-2\overrightarrow{a}\) là?
(3) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{u}=\left(-5;4\right)\), \(\overrightarrow{v}=-3\overrightarrow{j}\). tọa độ của vecto \(\overrightarrow{a}=2\overrightarrow{u}-5\overrightarrow{v}\) là?
(4) trong mặt phẳng tọa độ Oxy, cho hai điểm A (1;1), B (4;-7) và \(\overrightarrow{OM}=2\overrightarrow{OA}-5\overrightarrow{OB}\). tổng hoành độ và tung độ của điểm M là?
giúp mk vs ạ mk cần gấp thank
(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19
1, Trong mặt phẳng tọa độ Oxy , cho M(1;-1) . N (3;2) , P(0;-5) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC Tìm tọa độ điểm A
2, Trong mặt phẳng tọa độ Oxy , cho A(1;3) , B(-1;-2) , C(1;5) . Tọa độ D trên trục Ox sao cho ABCD là hình thang có 2 đấy AB và CD là ?
Trong mặt phẳng tọa độ Oxy , cho B(2;3) , C(-1;-2) Điểm M thỏa mãn \(\overrightarrow{2MB}+\overrightarrow{3MC}=\overrightarrow{0}\) Tìm tọa độ điểm M
Trong mặt phẳng tọa độ Oxy , cho vecto \(\overrightarrow{u}=\left(2;-4\right),\overrightarrow{a}=\left(1;-2\right),\overrightarrow{b}=\left(1;-3\right)\)Biết \(\overrightarrow{u}=m\overrightarrow{a}+n\overrightarrow{b}\) tính m - n bẳng ?
Trong mặt phẳng Oxy cho điểm \(A\left(2;1\right);B\left(6;5\right)\), tọa độ điểm M thuộc đoạn AB sao cho AM = 3 BM là...
Do M nằm trên đoạn AB nên \(\overrightarrow{AM}=-3\overrightarrow{BM}\)
Gọi \(M\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(x-2;y-1\right)\\\overrightarrow{BM}=\left(x-6;y-5\right)\end{matrix}\right.\)
\(\overrightarrow{AM}=-3\overrightarrow{BM}\Leftrightarrow\left\{{}\begin{matrix}x-2=-3\left(x-6\right)\\y-1=-3\left(y-5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\x=4\end{matrix}\right.\) \(\Rightarrow M=\left(5;4\right)\)
Trong mặt phẳng tọa độ Oxy, cho điểm \(A\left(1;2\right);B\left(-2;4\right);C\left(2;m\right)\). Hãy tìm m để 3 điểm A, B, C thẳng hàng ?
\(\overrightarrow{AB}\left(-3;2\right)\); \(\overrightarrow{AC}\left(1;m-2\right)\).
Ba điểm A, B, C thẳng hàng khi và chỉ khi:
\(\dfrac{1}{-3}=\dfrac{m-2}{2}\Leftrightarrow-3\left(m-2\right)=2\)\(\Leftrightarrow m=\dfrac{4}{3}\).
Bài 8: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:\(\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\left(t\in R\right)\) và điểm A(3;1).
1) Viết phương trình đường thẳng d’ đi qua A và vuông góc với đường thẳng d.
2) Tìm tọa độ giao điểm H của đường thẳng d và d’.
3) Xác định tọa độ điểm A’ đối xứng với A qua đường thẳng d.
4) Tìm tọa độ điểm M nằm trên đường thẳng d sao cho tổng khoảng cách MA+MO là nhỏ nhất.
5) Viết phương trình đường tròn (C) có tâm I nằm trên đường thẳng d và đi qua hai điểm A, O.
1: (d): x=-2-2t và y=1+2t nên (d) có VTCP là (-2;2)=(-1;1) và đi qua B(-2;1)
=>(d') có VTPT là (-1;1)
Phương trình (d') là;
-1(x-3)+1(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
2: (d) có VTCP là (-1;1)
=>VTPT là (1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+y+1=0
Tọa độ H là;
x+y+1=0 và -x+y+2=0
=>x=1/2 và y=-3/2
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
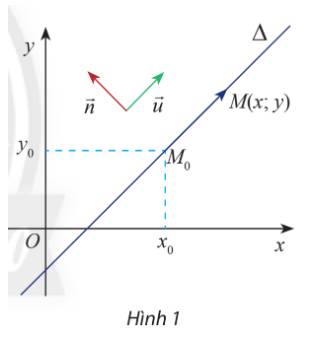
a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)
Trong mặt phẳng Oxy, cho đường thẳng \(d:x+y-2=0\) và 2 điểm \(A\left(1;3\right)\) và \(B\left(2;1\right)\). Biết điểm \(M\left(a;b\right)\), \(a>0\) thuộc d sao cho diện tích \(\Delta MAB=4\). Tính tổng của \(3a+5b\).
AB=căn 5
AB: (x-1)/1=(y-3)/-2
=>2x+y-5=0
M thuộc Δ nên M(m;2-m)
\(d\left(M;AB\right)=\dfrac{\left|m-3\right|}{\sqrt{5}}\)
\(S_{AMB}=\dfrac{1}{2}\cdot MH\cdot AB=4\)
=>|m-3|=8
=>m=11(nhận) hoặc m=-5(loại)
=>M(11;-9)
=>3a+5b=3*11+5*(-9)=-12
Trong mặt phẳng tọa độ Oxy, cho ba điểm \(I\left(2;4\right);B\left(1;1\right);C\left(5;5\right)\). Tìm điểm A sao cho I là tâm đường tròn nội tiếp tam giác ABC ?
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), chứng tỏ rằng điểm \(M\left( {x;y} \right)\) có tọa độ thỏa mãn phương trình:
\(ax + by + c = 0\) (với \(c = - a{x_0} - b{y_0}\))
\(\Delta \) nhận vectơ \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến, suy ra vectơ chỉ phương của \(\Delta \) là \(\overrightarrow u = (b; - a)\)
M và \({M_0}\) thuộc đường thẳng \(\Delta \) nên \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\), suy ra \(\left\{ \begin{array}{l}{x_0} - x = b\\{y_0} - y = - a\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - b\\y = {y_0} + a\end{array} \right.\)
Suy ra \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
Thay tọa độ điểm M vào phương trình \(ax + by + c = 0\) ta có:
\(a\left( {{x_0} - b} \right) + b\left( {{y_0} + a} \right) + c = \left( { - ab + ba} \right) + \left( {a{x_0} + b{y_0} + c} \right) = 0\) (đúng vì \( - a{x_0} - b{y_0} = c\))
Vậy \(M(x;y)\) thỏa mãn phương trình đã cho