11. Khoảng cách từ điểm M(1;-1) đến đg thẳng denta 3x -4y -17=0 là
A 2
B -18/5
C 2/5
D 10/ căn 5
Cho điểm A(2;5;3) và đường thẳng d: x - 1 1 = y - 1 1 = z + 2 1 . Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A đến (P) lớn nhất. Khoảng cách từ điểm M(1;2;-1) đến (P) bằng
A. 3 2
B. 11 18
C. 11
D. 11 18 18
Hình bình hành ABCD. Có A(2;1); C(6;7); và M(3;2) là điểm thuộc miền của hình bình hành. viết phương trình AD biết khoảng cách từ m đến CD bằng 5 làn khoảng cách từ M đến AB. D thuộc đường thẳng: x+y-11=0.
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
Trong mặt phẳng tọa độ Oxyz, cho mặt phẳng α : x − 2 y + 2 z − 11 = 0 và điểm M(0;0;1). Tính khoảng cách h từ điểm M đến mặt phẳng α .
A. h = 1.
B. h = 2.
C. h = 3.
D. h = 4.
Trong không gian Oxyz, tính khoảng cách từ điểm M 1 ; 3 ; 2 đến đường thẳng ∆ : x - 1 1 = y - 1 1 = z - 1
A. 2
B. 2
C. 2 2
D. 3
Chọn đáp án C
Đường thẳng ∆ đi qua điểm M 0 1 ; 1 ; 0 và có vec-tơ chỉ phương là u ⇀ = 1 ; 1 ; - 1
![]()
![]()
Khoảng cách từ điểm M đến đường thẳng ∆ là
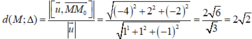
Trong mặt phẳng tọa độ Oxyz, cho mặt phẳng
( α ): x -2y + 2z - 11 = 0 và điểm M (0;1;1). Tính
khoảng cách h từ điểm M đến mặt phẳng ( α ).
A. h = 1
B. h = 2
C. h = 3
D. h = 4
một ô tô chạy từ địa điểm a đến địa điểm b với tốc độ 65km/h, cùng lúc dó 1 xe máy đi từ b về a với lận tốc 40km/h. Biết khoảng cách ab là 540 km và M là trung điểm của ab. Hỏi sau bao lâu thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách từ xe máy đến M
Theo bài ra ta có: quãng đường AB dài 540km => Nửa quãng đường AB dài 270km.
Gọi quãng đường ô tô và xe máy đã đi là S1 và S2.
Trong cùng một thời gian thì quãng đường tỉ lệ thuận với vận tốc.
\(\dfrac{S_1}{V_1}=\dfrac{S_2}{V_2}=t\)
Ta có phương trinh:
\(\dfrac{270-a}{65}=\dfrac{270-a}{40}\Rightarrow t=\dfrac{270}{90}=3h\)
Vậy sau 3 giờ thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách xe máy đến M
tìm điểm M thuộc đồ thị hàm số \(y=\dfrac{2x+1}{x-1}\) sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến trục hoành.
Đồ thị hàm nhận \(x=1\) là tiệm cận đứng
Gọi \(M\left(a;b\right)\Rightarrow b=\dfrac{2a+1}{a-1}\)
Khoảng cách từ M đến trục hoành: \(\left|y_M\right|=\left|b\right|\)
Khoảng cách từ M đến tiệm cận đứng: \(\left|x_M-1\right|=\left|a-1\right|\)
Ta được hệ: \(\left\{{}\begin{matrix}b=\dfrac{2a+1}{a-1}\\\left|b\right|=\left|a-1\right|\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(0;-1\right);\left(4;3\right)\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(0;-1\right)\\M\left(4;3\right)\end{matrix}\right.\)
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15