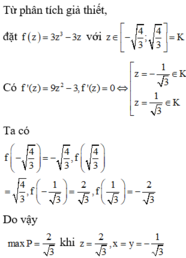cho x,y thay đổi thỏa mãn x >=2 ; x+y >=3. CMR: x2 + y2 >=5

Những câu hỏi liên quan
1, cho x, y thay đổi thỏa mãn: x^2+y^2=2
tìm min max của P=2(x^3+y^3)-3xy
2, cho x, y thay đổi thỏa mãn x^2+y^2=1
tìm min max của P=( 2x^2+12xy)/ (1+2xy+2y^2)
1. Đặt x = √2.cosα và y = √2.sinα (với α trên [0,3π/2])
Ta có: P = 4√2(sinα + cosα)(1 - sinαcosα) - 6sinαcosα
Đặt t = sinα + cosα = √2.sin(α + π/4) có |t| ≤ √2, nên sinαcosα = (t^2 - 1)/2
suy ra P = -2√2.t^3 - 3t^2 + 6√2.t + 3.
Đến đây bạn áp dụng P' = 0 rồi xét các gtrị cực trị.
2. Đặt x = cosα và y = sinα (với α trên [0,3π/2])
Biến đổi P = (6sin2α + cos2α + 1) / (3 + sin 2α - cos 2α)
Mặt khác lại có (cos2α)^2 + (sin 2α)^2 = 1.
Ta áp dụng P' = 0 tiếp.
Đúng 0
Bình luận (0)
Cho x;y thay đổi thỏa mãn x >=2 ; x+y >=3. CMR: x2 + y2 >= 5
sao đa số mọi người toàn copy lên mạng hoặc vô câu hỏi tương tự vại
Đúng 0
Bình luận (0)
cho x,y,z thay đổi thỏa mãn 0< x,y,z<2
cm: 2( x+y+z)-(xy+yz+xz)<4
Bài 1 :Cho 2 số dương x,y thỏa mãn điều kiện x+yle1. Chứng minhx^2-frac{3}{4x}-frac{x}{y}lefrac{-9}{4}Bài 2 : Cho 2 số thực x,y thay đổi thỏa mãn điều kiện x+yge1và x0Tìm giá trị nhỏ nhất của biểu thức My^2+frac{8x^2+y}{4x}bài 3: cho 3 số dương x,y,z thay đổi luôn thỏa mãn điều kiện x+y+z1. Tìm giá trị lớn nhất của biểu thức:Pdfrac{x}{x+1}+dfrac{y}{y+1}+dfrac{z}{z+1}
Đọc tiếp
Bài 1 :Cho 2 số dương x,y thỏa mãn điều kiện \(x+y\le1\). Chứng minh\(x^2-\frac{3}{4x}-\frac{x}{y}\le\frac{-9}{4}\)
Bài 2 : Cho 2 số thực x,y thay đổi thỏa mãn điều kiện x+y\(\ge1\)và x>0
Tìm giá trị nhỏ nhất của biểu thức \(M=y^2+\frac{8x^2+y}{4x}\)
bài 3: cho 3 số dương x,y,z thay đổi luôn thỏa mãn điều kiện x+y+z=1. Tìm giá trị lớn nhất của biểu thức:\(P=\dfrac{x}{x+1}+\dfrac{y}{y+1}+\dfrac{z}{z+1}\)
3: \(P=\dfrac{x}{\left(x+y\right)+\left(x+z\right)}+\dfrac{y}{\left(y+z\right)+\left(y+x\right)}+\dfrac{z}{\left(z+x\right)+\left(z+y\right)}\le\dfrac{1}{4}\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}\right)+\dfrac{1}{4}\left(\dfrac{y}{y+z}+\dfrac{y}{y+x}\right)+\dfrac{1}{4}\left(\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)=\dfrac{3}{2}\).
Đẳng thức xảy ra khi x = y = x = \(\dfrac{1}{3}\).
Đúng 1
Bình luận (0)
cho hai số dương x, y thay đổi thỏa mãn XY = 2. Tìm GTNN của biểu thức \(M=\dfrac{1}{x}+\dfrac{2}{y}+\dfrac{3}{2x+y}\)
\(M=\dfrac{2x+y}{xy}+\dfrac{3}{2x+y}=\dfrac{2x+y}{2}+\dfrac{3}{2x+y}=\dfrac{3\left(2x+y\right)}{16}+\dfrac{3}{2x+y}+\dfrac{5}{16}\left(2x+y\right)\ge2\sqrt{\dfrac{3}{16}.3}+\dfrac{5}{16}.2\sqrt{2xy}=\dfrac{3}{2}+\dfrac{5}{4}=\dfrac{11}{4}\).
Đẳng thức xảy ra khi x = 1; y = 2.
Đúng 2
Bình luận (0)
\(M=\dfrac{2x+y}{xy}+\dfrac{3}{2x+y}=\dfrac{2x+y}{2}+\dfrac{3}{2x+y}\)
\(M=\dfrac{3\left(2x+y\right)}{16}+\dfrac{3}{2x+y}+\dfrac{5\left(2x+y\right)}{16}\ge2\sqrt{\dfrac{9\left(2x+y\right)}{16\left(2x+y\right)}}+\dfrac{5}{16}.2\sqrt{2xy}=\dfrac{11}{4}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(1;2\right)\)
Đúng 1
Bình luận (0)
Ta có: \(M=\dfrac{2x+y}{xy}+\dfrac{3}{2x+y}=\dfrac{2x+y}{2}+\dfrac{3}{2x+y}\)
\(=\left(\dfrac{3}{8}\dfrac{2x+y}{2}+\dfrac{3}{2x+y}\right)+\dfrac{5}{8}\dfrac{2x+y}{2}\)
Có: \(\dfrac{3}{8}\dfrac{2x+y}{2}+\dfrac{3}{2x+y}\ge2\sqrt{\dfrac{3}{8}\dfrac{2x+y}{2}\dfrac{3}{2x+y}}=\dfrac{3}{2}\)
Dấu '=' xảy ra <=> \(\dfrac{3}{8}\dfrac{2x+y}{2}=\dfrac{3}{2x+y}\)
Có: \(\dfrac{5}{8}\dfrac{2x+y}{2}\ge\dfrac{5}{8}\sqrt{2xy}=\dfrac{5}{4}\)
Dấu '=' xảy ra <=> 2x=y và xy=2
\(\Rightarrow M\ge\dfrac{3}{2}+\dfrac{5}{4}=\dfrac{11}{4}\)
Dấu '=' xảy ra <=> x=1, y=2
Vậy GTNN của M là 11/4 <=> x=1;y=2
Đúng 1
Bình luận (0)
Cho hai số dương x,y thay đổi thỏa mãn xy=2. Tìm GTNN của biểu thức M=\(\dfrac{1}{x}+\dfrac{2}{y}+\dfrac{3}{2x+y}\)
Ta có:
\(M=\dfrac{2x+y}{xx}+\dfrac{3}{2x+y}=\dfrac{2x+y}{2}+\dfrac{3}{2x+y}\)
\(=\left(\dfrac{3}{8}\dfrac{2x+y}{2}+\dfrac{3}{2x+y}\right)+\dfrac{5}{8}\dfrac{2x+y}{2}\)
Có: \(\dfrac{3}{8}\dfrac{2x+y}{2}+\dfrac{3}{2x+y}\ge2\sqrt{\dfrac{3}{8}\dfrac{2x+y}{2}\dfrac{3}{2x+y}}=\dfrac{3}{2}\)
Dấu '=' xảy ra \(\Leftrightarrow\dfrac{3}{8}\dfrac{2x+y}{2}=\dfrac{3}{2x+y}\)
Có: \(\dfrac{5}{8}\dfrac{2x+y}{2}\ge\dfrac{5}{8}\sqrt{2xy}=\dfrac{5}{4}\)
Dấu '=' xảy ra \(\Leftrightarrow2x=y,xy=2\)
\(\Rightarrow M\ge\dfrac{3}{2}+\dfrac{5}{4}=\dfrac{11}{4}\)
Dấu '=' xảy ra \(\Leftrightarrow x=1,y=2\)
Vậy GTNN của M là \(\dfrac{11}{4}\Leftrightarrow x=1,y=2\)
Đúng 0
Bình luận (1)
Cho hai số thực x,y khác 0 thay đổi và thỏa mãn đk \(\left(x+y\right)xy=x^2+y^2-xy\). GTLN của bthuc \(M=\dfrac{1}{x^3}+\dfrac{1}{y^3}\)
cho x, y là các số thực thay đổi thỏa mãn x^2+y^2-24=6x+8y. Tìm giá trị lớn nhất của biểu thức P=3x+4y
Cho ba số thực x, y, z thay đổi thỏa mãn
x
+
y
+
z
0
x
2
+
y
2
+...
Đọc tiếp
Cho ba số thực x, y, z thay đổi thỏa mãn x + y + z = 0 x 2 + y 2 + z 2 = 2 Tìm giá tri lớn nhất của biểu thức P = x 3 + y 3 + z 3
A. 3 4
B. 2 3
C. 1
D. - 3 2