Xét tam giác BDI có: IK và DH là 2 đường cao; IK cắt DH tại A => A  là trực tâm của tam giác DIB => BA vuông góc với ID

Mà BA vuông góc với BC (do tam giác ABC vuông tại B)

=> BC // ID => góc BCA = góc IDC (do ở vị trí SLT)              (1)

+) Để tam giác BID đều thì tam giác BID cân tại D và góc BDI = 60^o

tam giác BDI cân tại D <=>  DH là đường cao đồng thời là đường phân giác => góc IDC = góc CDB = góc BDI/2

mà góc BDI = 60 độ => góc IDC = 30^o                                   (2)

từ (1)(2) => góc BCA = 30^o

Vậy để tam giác BDI đều thì tam giác ABC phải thoả mãn góc BCA = 30 độ

Giải giúp mình với ạ

b: AH=14,4cm

BH=19,2cm

CH=10,8cm

a, \(AB=\sqrt{BC^2-AC^2}=24\left(cm\right)\left(pytago\right)\)

\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\)

b, Áp dụng HTL: \(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=19,2\left(cm\right)\\CH=\dfrac{AC^2}{BC}=10,8\left(cm\right)\\AH=\sqrt{BH\cdot CH}=14,4\left(cm\right)\end{matrix}\right.\)

Giúp đi mà mấy bro ơi

b: AB=24cm

AH=14,4(cm)

BH=19,2(cm)

CH=10,8(cm)

Đề sai rồi bạn

b: BH=19,2cm

AH=14,4cm

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có

góc B chung

=>ΔBAC đồng dạng với ΔBHA

b: ΔBAC đồng dạng vơi ΔBHA

=>BA/BH=BC/BA

=>BA^2=BH*BC

c: ΔABC vuông tại A có AH là đường cao

nên AH*BC=AB*AC

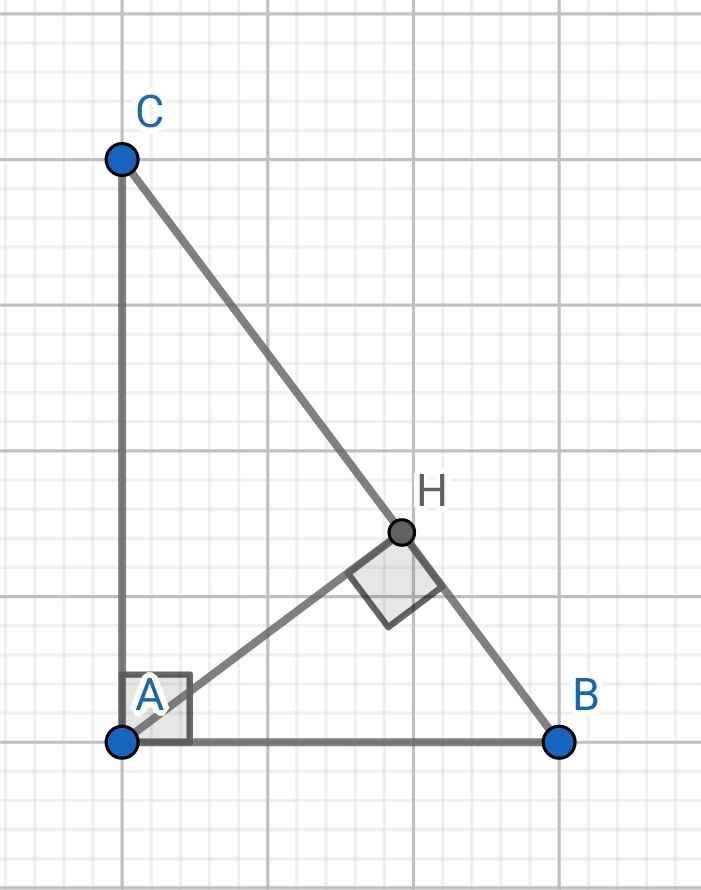
a) Xét hai tam giác vuông: ∆ABC và ∆HBA có:

∠B chung

⇒ ∆ABC ∽ ∆HBA (g-g)

b) ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10

Do ∆ABC ∽ ∆HBA (cmt)

⇒ AC/AH = BC/AB

⇒ AH = AB.AC/BC

= 6.8/10

= 4,8 (cm)

∆ABH vuông tại H

⇒ AB² = AH² + BH² (Pytago)

⇒ BH² = AB² - AH²

= 6² - (4,8)²

= 12,96

⇒ BH = 3,6 (cm)

a) Ta có:

- Góc A của tam giác ABC là góc vuông, nên ta có thể tính được độ dài đoạn thẳng AH bằng cách sử dụng định lí Pythagoras: AH = sqrt(AB^2 + AC^2) = sqrt(6^2 + 8^2) = 10.

- Góc A của tam giác ABC cũng là góc giữa đường cao AH và cạnh huyền BC, nên ta có thể tính được tỉ số giữa độ dài đoạn thẳng AH và độ dài cạnh huyền BC: AH/BC = AC/AB = 8/6 = 4/3.

- Từ tỉ số này, ta có thể suy ra rằng tam giác ABC đồng dạng với tam giác HBA (vì cả hai tam giác có cùng một góc và tỉ số giữa các cạnh tương ứng bằng nhau).

b) Để tính độ dài các cạnh BC, AH, BH, ta có thể sử dụng các công thức sau:

- Độ dài cạnh BC: BC = AB/AC * AH = 6/8 * 10 = 15/2 = 7.5.

- Độ dài đoạn thẳng BH: BH = sqrt(AH^2 - AB^2) = sqrt(10^2 - 6^2) = 8.

- Độ dài đoạn thẳng AH đã được tính ở trên: AH = 10.

Vậy độ dài các cạnh BC, AH, BH lần lượt là 7.5cm, 10cm, 8cm.

Xét ΔAHB vuông tại H và ΔCAB vuông tại A có

góc B chung

=>ΔAHB đồng dạng với ΔCAB

=>BA/BC=BH/BA

=>BA^2=BH*BC