Đối với mỗi phương trình sau, hãy tìm các giá trị của m để phương trình có nghiệm; tính nghiệm của phương trình theo m :
a) \(mx^2+\left(2m-1\right)x+m+2=0\)
b) \(2x^2-\left(4m+3\right)x+2m^2-1=0\)
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm, tính nghiệm của phương trình theo m: m x 2 + (2m – 1)x + m + 2 = 0
m x 2 + (2m – 1)x + m + 2 = 0 (1)
*Nếu m = 0, ta có (1) ⇔ -x + 2 = 0 ⇔ x = 2
*Nếu m ≠ 0 thì (1) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có : ∆ = 2 m - 1 2 – 4m(m + 2) = 4 m 2 – 4m + 1 – 4 m 2 – 8m
= -12m + 1
∆ ≥ 0 ⇔ -12m + 1 ≥ 0 ⇔ m ≤ 1/12
Vậy khi m ≤ 1/12 thì phương trình đã cho có nghiệm.
Giải phương trình (1) theo m :
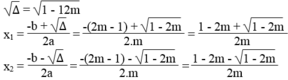
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm, tính nghiệm của phương trình theo m: 2 x 2 – (4m + 3)x + 2 m 2 – 1 = 0
2 x 2 – (4m + 3)x + 2 m 2 – 1 = 0 (2)
Phương trình (2) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có: ∆ = - 4 m + 3 2 – 4.2(2 m 2 – 1)
= 16 m 2 + 24m + 9 – 16 m 2 + 8 = 24m + 17
∆ ≥ 0 ⇔ 24m + 17 ≥ 0 ⇔ m ≥ -17/24
Vậy khi m ≥ -17/24 thì phương trình đã cho có nghiệm.
Giải phương trình (2) theo m:

Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm kép: 3 x 2 + (m + 1)x + 4 = 0
Phương trình 3 x 2 + (m + 1)x + 4 = 0 có nghiệm kép khi và chỉ khi ∆ = 0
Ta có : ∆ = m + 1 2 – 4.3.4 = m 2 + 2m + 1 – 48 = m 2 + 2m – 47
∆ = 0 ⇔ m 2 + 2m – 47 = 0
Giải phương trình m 2 + 2m – 47 = 0. Ta có:
∆ m = 2 2 – 4.1.(-47) = 4 + 188 = 192 > 0
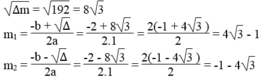
Vậy với m = 4 3 – 1 hoặc m = -1 - 4 3 thì phương trình đã cho có nghiệm kép.
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm kép: m x 2 – 2(m – 1)x + 2 = 0
Phương trình m x 2 – 2(m – 1)x + 2 = 0 có nghiệm kép khi và chỉ khi m ≠ 0 và Δ = 0
Ta có: ∆ = - 2 m - 1 2 – 4.m.2 = 4( m 2 – 2m + 1) – 8m
= 4( m 2 – 4m + 1)
∆ = 0 ⇔ 4( m 2 – 4m + 1) = 0 ⇔ m 2 – 4m + 1 = 0
Giải phương trình m 2 – 4m + 1 = 0. Ta có:
∆ m = - 4 2 – 4.1.1 = 16 – 4 = 12 > 0
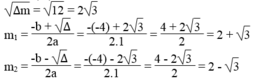
Vậy với m = 2 + 3 hoặc m = 2 - 3 thì phương trình đã cho có nghiệm kép.
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm, tính nghiệm của phương trình theo m:
a. mx2 + (2m – 1)x + m + 2 = 0 b. 2x2 - (4m +3)x + 2m2 - 1 = 0
c. x2 – 2(m + 3)x + m2 + 3 = 0 d. (m + 1)x2 + 4mx + 4m +1 = 0
\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)
Cho phương trình: \(x^2-2\left(3m+2\right)x+2m^2-3m+5=0\)
a. Giải phương trình với m = -2
b. Tìm các giá trị của m để phương trình trên có một trong các nghiệm bằng 1
c. Tìm các giá trị của m để phương trình trên có nghiệm kép.
Đối với mỗi phương trình sau, hãy tìm các giá trị của m để phương trình có nghiệm kép:
a) \(mx^2-2\left(m-1\right)x+2=0\)
b) \(3x^2+\left(m+1\right)x+4=0\)
a) m \(\ne\)0; \(\Delta'=\left(m-1\right)^2-2m=0\Leftrightarrow m^2-4m+1=0\Leftrightarrow\left(m-2\right)^2=3\)
=>m=2+ \(\sqrt{3}\) hoặc m=2 -\(\sqrt{3}\) (TM)
b) \(\Delta=\left(m+1\right)^2-4.3.4=0\)=>m =-1 +4\(\sqrt{3}\) hoặc m = -1 - 4\(\sqrt{3}\)
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm kép :
a) \(mx^2-2\left(m-1\right)x+2=0\)
b) \(3x^2+\left(m+1\right)x+4=0\)
cho phương trình : \(2x^2-\left(m+3\right)x+m=0\) (1)
a, chứng tỏ phương trình (1) có nghiệm với mọi giá trị của m
b, gọi \(x_1,x_2\) là các nghiệm của phương trình (1).Tìm giá trị nhỏ nhất của biểu thức sau A= trị tuyệt đối của \(x_1-x_2\)
a: \(\text{Δ}=\left[-\left(m+3\right)\right]^2-4\cdot2\cdot m\)
\(=\left(m+3\right)^2-8m\)
\(=m^2-2m+9=\left(m-1\right)^2+8>0\forall m\)
=>Phương trình (1) luôn có hai nghiệm phân biệt
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{m+3}{2}\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{m}{2}\end{matrix}\right.\)
\(A=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}\)
\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\dfrac{1}{4}\left(m+3\right)^2-4\cdot\dfrac{m}{2}}\)
\(=\sqrt{\dfrac{1}{4}\left(m^2+6m+9\right)-2m}\)
\(=\sqrt{\dfrac{1}{4}m^2+\dfrac{3}{2}m+\dfrac{9}{4}-2m}\)
\(=\sqrt{\dfrac{1}{4}m^2-\dfrac{1}{2}m+\dfrac{9}{4}}\)
\(=\sqrt{\dfrac{1}{4}\left(m^2-2m+9\right)}\)
\(=\sqrt{\dfrac{1}{4}\left(m^2-2m+1+8\right)}\)
\(=\sqrt{\dfrac{1}{4}\left(m-1\right)^2+2}>=\sqrt{2}\)
Dấu '=' xảy ra khi m-1=0
=>m=1