vẽ ΔABC có AB= 6cm; góc B=58 độ ; Å- 62 độ. tính số đo góc ngoài tại đỉnh c?

Những câu hỏi liên quan
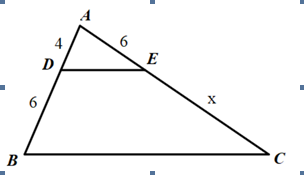
Cho hình vẽ, biết ΔABC có DE=BC , AB = 4cm , DB = 6cm AE = 6cm . Tìm x
\(DE=EC\\ \Rightarrow DE//BC\\ \Rightarrow\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{6}=\dfrac{6}{x}\\ \Rightarrow x=9\)
Đúng 1
Bình luận (3)
Cho ΔABC vuông tại A có AB = 8cm, AC = 6cm. Vẽ phân giác trong BD và CE. Tính các đoạn thẳng AE,AD,EF,DC.
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=8^2+6^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AD}{8}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{4}=\dfrac{CD}{5}\)
mà AD+CD=AC=6cm(Do D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{4}=\dfrac{CD}{5}=\dfrac{AD+CD}{4+5}=\dfrac{6}{9}=\dfrac{2}{3}\)
=>\(AD=4\cdot\dfrac{2}{3}=\dfrac{8}{3}\left(cm\right);CD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)
Xét ΔCAB có CE là phân giác
nên \(\dfrac{AE}{AC}=\dfrac{BE}{BC}\)
=>\(\dfrac{AE}{6}=\dfrac{BE}{10}\)
=>\(\dfrac{AE}{3}=\dfrac{BE}{5}\)
mà AE+BE=AB=8cm(E nằm giữa A và B)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AE}{3}=\dfrac{BE}{5}=\dfrac{AE+BE}{3+5}=\dfrac{8}{8}=1\)
=>\(AE=3\cdot1=3cm;BE=5\cdot1=5cm\)
Đúng 0
Bình luận (0)
ΔABC vuông tại A,Có I là trung điểm Bc.
A)Cho Ab=6cm ; AC=8cm.Tính AI
B) Từ I kẻ IH ⊥ AB ; IK ⊥ AC.Chứng minh tứ giác AHIK là hình chữ nhật.
C)Vẽ E đ/x I qua K. Chứng minh tứ giác AICE là hình thoi
D) Tính diện tích ΔABC
a: AI=5cm
b: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
Đúng 0
Bình luận (0)
cho ΔABC vuông tại A, có AB = 6cm, AC = 8cm. Vẽ đường cao AH(H ϵ BC)
a) tính dt Δvuông ABC
b) vẽ p/g AD của góc A( D ϵ BC). tính DB,DC
c) C/m: α)ΔABC và ΔHBA đồng dạng
β)AB2 = BH.BC
γ)1/AH2 = 1/AB2 + 1/AC2
giúp mik vs mik đang cần gấp ạ
a. Diện tích của Δ ABC là:
\(\dfrac{1}{2}\) . 6 . 8 = 24 cm2
b. Ta có: Δ ABC vuông tại A
Theo đ/lí Py - ta - go
BC2 = AB2 + AC2
BC2 = 62 + 82
BC2 = 100
\(\Rightarrow\) BC = \(\sqrt{100}\) = 10 cm
Vì AD là tia phân giác của \(\widehat{A}\)
\(\dfrac{AB}{AC}=\dfrac{DB}{DC}\)
\(\Rightarrow\) \(\dfrac{6}{8}\) = \(\dfrac{DB}{10-DB}\)
\(\Rightarrow\) \(\dfrac{3}{4}=\dfrac{DB}{10-DB}\)
\(\Rightarrow\) 3 . (10 - DB) = 4DB
\(\Rightarrow\) 30 - 3DB - 4DB = 0
\(\Rightarrow\) 30 - 7DB = 0
\(\Rightarrow\) DB = \(\dfrac{30}{7}\) \(\approx\) 4,3 cm
Ta có: DC = 10 - DB
\(\Rightarrow\) DC = 10 - 4,3
\(\Rightarrow\) DC = 5,7 cm
c. Xét ΔABC và ΔHBA:
\(\widehat{A}=\widehat{H}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔABC \(\sim\) ΔHBA (g.g)
Ta có: ΔABC \(\sim\) ΔHBA
\(\dfrac{AB}{HB}=\dfrac{BC}{BA}\)
\(\Rightarrow\) AB2 = BH . BC
Vì ΔABC vuông tại A
SΔABC = \(\dfrac{AH.BC}{2}\) = \(\dfrac{AB.AC}{2}\) \(\Rightarrow\) AB . AC
\(\Leftrightarrow\) AH = \(\dfrac{AB.AC}{BC}\) = \(\Leftrightarrow\) \(\dfrac{1}{AH}\) = \(\dfrac{AH}{AB.AC}\)
\(\Leftrightarrow\) \(\dfrac{1}{AB^2}\) = \(\dfrac{BC^2}{AB^2.AC^2}\)
Mặt khác theo đ/lí Py - ta - go:
BC2 = AB2 + AC2
\(\Rightarrow\) \(\dfrac{1}{AH^2}\) = \(\dfrac{AB^2+AC^2}{AB^2.ÂC^2}\) = \(\dfrac{1}{AB^2}\) + \(\dfrac{1}{AC^2}\)
\(\Rightarrow\) \(\dfrac{1}{AH^2}\) = \(\dfrac{1}{AB^2}\) + \(\dfrac{1}{AC^2}\) (dpcm)
nhớ tick cho cj nha
Đúng 0
Bình luận (0)
cho ΔABC vuông tại A ,vẽ trung tuyến AM,trên tia đối của tia MA lấy điểm E sao cho ME=MA .chứng minh
a/ ΔMBA=ΔMCE
b/AB//CE
c/giả sử AB=6cm,AC=8cm,BC=10cm.So sánh các góc của ΔABC
a: Xét ΔMBA và ΔMCE có
MB=MC
góc BMA=góc CME
MA=ME
=>ΔMBA=ΔMCE
b: ΔMBA=ΔMCE
=>góc MBA=góc MCE
=>AB//CE
c: AB<AC<CB
=>góc C<góc B<góc A
Đúng 0
Bình luận (0)
cho tam giác ABC vuông ở A , có AB=6cm, AC=8cm. vẽ đường cao AH
a, tính BC
b, chứng minh ΔABC đồng dạng với ΔAHB
c, tính diện tích ΔABH và ΔBDC
a/ Áp dụng định lý Pytago vào \(\Delta ABC\) vuông tại \(A\):
\(\to BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=\sqrt{100}=10\) (cm)
b/ Xét \(\Delta BAC\) và \(\Delta BHA\):
\(\widehat{B}:chung\)
\(\widehat{BAC}=\widehat{BHA}(=90^\circ)\)
\(\to \Delta BAC\backsim \Delta BHA\) (g-g)
c/ \(AH\cdot BC=AC\cdot AB\)
\(\to AH=\dfrac{AC\cdot AB}{BC}=\dfrac{6\cdot 8}{10}=4,8\) (cm)
Áp dụng định lý Pytago vào \(\Delta AHB\) vuông tại \(H\)
\(\to BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6\) (cm)
\(S_{\Delta AHB}=\dfrac{1}{2}\cdot AH\cdot BH=\dfrac{1}{2}\cdot 4,8\cdot 3,6=8,64(cm^2)\)
Thiếu điểm D nên không tính được diện tích tam giác BDC
Đúng 0
Bình luận (1)
Cho ΔABC cân tại A có AB=AC=6cm, BC=4cm. Tính bán kính đường tròn tìm ngoại tiếp ΔABC
Gọi O là tâm đường tròn ngoại tiếp ΔABC
Gọi H là giao của AO với BC
AB=AC
OB=OC
Do đó: AO là trung trực của BC
=>AH là trung trực của BC
=>H là trung điểm của BC
HB=HC=4/2=2cm
Kẻ giao của AO với (O) là D
=>AD là đường kính của (O)
Xét (O) có
ΔABD nội tiếp
ADlà đường kính
Do đó: ΔBAD vuông tại B
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>\(AH^2=6^2-2^2=32\)
=>\(AH=4\sqrt{2}\left(cm\right)\)
Xét ΔBAD vuông tại B có BH là đường cao
nên AB^2=AH*AD
=>\(AD=\dfrac{6^2}{4\sqrt{2}}=\dfrac{9}{\sqrt{2}}\left(cm\right)\)
=>\(R=\dfrac{AD}{2}=\dfrac{9}{2\sqrt{2}}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho hình vẽ sau. Biết AD⊥BC tại D,AB=6cm AD=4,8cm CD=6,4cm.
A,Tính BD và AC
B,Chứng minh ΔABC vuông
Cho hình vẽ sau. Biết AD⊥BC tại D,AB=6cm AD=4,8cm CD=6,4cm.
A,Tính BD và AC
B,Chứng minh ΔABC vuông
Bạn cập nhật lại hình vẽ nhé bạn
Đúng 0
Bình luận (0)
hình e tự vẽ
a) xét tg ABD vuông tại D
\(\Rightarrow BD^2=AB^2-AD^2=6^2-4,8^2\\ \Rightarrow BD=\sqrt{6^2-4,8^2}=3,6cm\)
xét tg ADC vuông tại D
\(\Rightarrow AC^2=AD^2+DC^2\\ \Rightarrow AC=\sqrt{4,8^2+6,4^2}=\sqrt{64}=8cm\)
b) có BC =BD+DC==3,6+6,4=10cm
mà \(10^2=6^2+8^2\\ \Leftrightarrow BC^2=AB^2+AC^2\)
=> tg ABC vg tại A
bài này chủ yếu dùng pytago thôi áp dụng vào là làm dễ
Đúng 0
Bình luận (0)



















