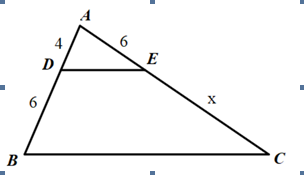
\(DE=EC\\ \Rightarrow DE//BC\\ \Rightarrow\dfrac{AD}{DB}=\dfrac{AE}{EC}\Rightarrow\dfrac{4}{6}=\dfrac{6}{x}\\ \Rightarrow x=9\)
Đúng 1
Bình luận (3)
Các câu hỏi tương tự
23 tháng 3 2023 lúc 22:19
Cho ΔABC có đường phân giác AD (D∈BC). Biết AB=4cm, AC= 6cm, DB=3cm. Tính DC,BC
GIÚP MIK VS
cho ΔABC vuông tại A có AB=6cm, AC=8cm. AD là tia phân giác của ∠BAC( D∈BC)
a) tính tỉ số \(\dfrac{BD}{DC}\)và độ dài đoạn thẳng BC, DB, DC
b) kẻ DE⊥AB. Tính độ dài DE, AE và diện tích tứ giác AEDC
c) gọi O là giao điểm AD và CE. Qua O kẻ đg thẳng // AC cắt BC và AB lần lượt tại M, N. C/m: OM=ON
Cho ΔABC có AB = 5 cm, AC =7,5cm, BC =6cm. Trên AB, AC lấy điểm D,E sao cho AD= 3cm, AE =2cm
a) Chứng minh ΔADE ~ ΔACB
b) Tính DE
Cho tam giác ABC, có AB=4cm, AC=6cm, BC=5cm. Kẻ đường phân giác góc BAC giao BC tại D.
a)Tính BD,CD
b)Từ D kẻ DE//AC (E\(\in AB\)). Chứng minh AE=DE
c)Tính AE
16 tháng 3 2021 lúc 18:24
Cho hình bình hành ABCD có AB = 6cm, AD = 8cm. Trên cạnh CD lấy điểm E sao cho DE = 4cm. Đường thẳng AE cắt BD tại O và cắt đường thẳng BC tại F. Tính độ dài đoạn thẳng FC.
Xem chi tiết
cho tam giác ABC vuông ở A , có AB=6cm, AC=8cm. vẽ đường cao AH a, tính BC b, chứng minh ΔABC đồng dạng với ΔAHB c, chứng minh AB2=BH.BC. Tính BH, HC d, vẽ phân giác AD (D ϵ BC) tính DB
Cho ∆ABC có EF // BC (E thuộc AB, F thuộc AC), đường phân giác AD cắt BC tại D, biết AE = 6cm, EB = 3cm, FC = 4cm, DC = 6cm. AF = x, BD = y, EF = z a) Tính x, y b) Tính z
cho hình vẽ AB = 6cm, AM =4cm,AN=6cm,AC=9cm.chứng minh MN // BC
cho ΔABC vuông tại A, có AB = 6cm, AC = 8cm. Vẽ đường cao AH(H ϵ BC)
a) tính dt Δvuông ABC
b) vẽ p/g AD của góc A( D ϵ BC). tính DB,DC
c) C/m: α)ΔABC và ΔHBA đồng dạng
β)AB2 = BH.BC
γ)1/AH2 = 1/AB2 + 1/AC2
giúp mik vs mik đang cần gấp ạ