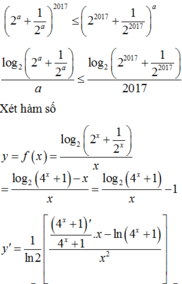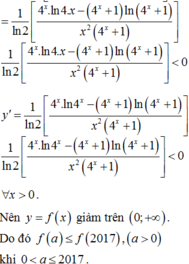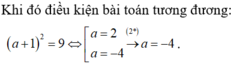Tìm tất cả các số thực a; b; c thỏa mãn a+b+c=3/a+4/b+9/c

Những câu hỏi liên quan
a) Tìm tất cả các số thực x sao cho x2 = 4.
b) Tìm tất cả các số thực x sao cho x3 = - 8.
a) \({x^2} = 4 = {2^2} = {\left( { - 2} \right)^2} \Leftrightarrow x = \pm 2\)
b) \({x^3} = - 8 = {\left( { - 2} \right)^3} \Leftrightarrow x = - 2.\)
- Chú ý:
Trong toán học, căn bậc chẵn của một số là một số lớn hơn 0. Do đó số âm không có căn bậc chẵn.
Đúng 0
Bình luận (0)
tìm tập hợp tất cả các ước của 30. Tính tổng các ước thực sự ( ước thực sự của số a là các ước khác a )
Tìm tất cả các giá trị thực của tham số a để biểu thức
B
log
3
2
−
a
có nghĩa A. a 2 B. a 3 C.
a
≤
2
D.
x
2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số a để biểu thức B = log 3 2 − a có nghĩa
A. a > 2
B. a = 3
C. a ≤ 2
D. x = 2
Đáp án D
Phương pháp: Biểu thức log a b có nghĩa khi 0 < a ≠ 1 ; b > 0
Cách giải: Biểu thức B = log 3 2 − a có nghĩa khi 2 − a > 0 ⇔ a < 2
Sai lầm và chú ý: Ở bài toán này ta chỉ cần chú ý đến điều kiện có nghĩa của hàm số logarit và giải bất phương trình để tìm x.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số a(a0) thỏa mãn
2
a
+
1
2
a
2017
≤
2
2017
+
1
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số a(a>0) thỏa mãn 2 a + 1 2 a 2017 ≤ 2 2017 + 1 2 2017 a
A. 0 < a < 1
B. 1 < a < 2017
C. a ≥ 2017
D. 0 < a ≤ 2017
Đáp án C
Ta có 2 a + 1 2 a 2017 ≤ 2 2017 + 1 2 2017 a ⇔ 1 + 4 a 2017 ≤ 1 + 4 2017 a ⇔ ln 1 + 4 a a ≤ ln 1 + 4 2017 2017
Xét hàm số f t = ln 1 + 4 t t với t ∈ 0 ; + ∞ ⇒ Hàm số nghịch biến trên khoảng 0 ; + ∞
Mà ln 1 + 4 a a ≤ ln 1 + 4 2017 2017 ⇔ f a ≤ f 2017 suy ra a ≥ 2017
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số a (a 0) thỏa mãn
2
a
+
1
2
1
2017
≤
2
2017
+
1
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số a (a >0) thỏa mãn 2 a + 1 2 1 2017 ≤ 2 2017 + 1 2 2017 a
A. 0< a≤ 2017.
B. 1< a< 2017.
C. a ≥2017.
D. 0< a< 1.
Tìm tất cả các số thực a; b; c thỏa mãn a+b+c=3/a=4/b=9/c
Ta có: \(\dfrac{3}{a}=\dfrac{4}{b}=\dfrac{9}{c}\)
nên \(\dfrac{3}{a}=\dfrac{4}{b}=\dfrac{9}{c}=\dfrac{3+4+9}{a+b+c}=\dfrac{16}{a+b+c}\)
Ta có: \(a+b+c=\dfrac{3}{a}=\dfrac{4}{b}=\dfrac{9}{c}\)
\(\Leftrightarrow a+b+c=\dfrac{16}{a+b+c}\)
\(\Leftrightarrow\left(a+b+c\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b+c=4\\a+b+c=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3}{a}=\dfrac{4}{b}=\dfrac{9}{c}=4\\\dfrac{3}{a}=\dfrac{4}{b}=\dfrac{9}{c}=-4\end{matrix}\right.\)
Trường hợp 1: \(\dfrac{3}{a}=\dfrac{4}{b}=\dfrac{9}{c}=4\)
nên \(\left\{{}\begin{matrix}a=\dfrac{3}{4}\\b=1\\c=\dfrac{9}{4}\end{matrix}\right.\)
Trường hợp 2: \(\dfrac{3}{a}=\dfrac{4}{b}=\dfrac{9}{c}=-4\)
nên \(\left\{{}\begin{matrix}a=\dfrac{-3}{4}\\b=-1\\c=\dfrac{-9}{4}\end{matrix}\right.\)
Vậy: \(\left(a,b,c\right)\in\left\{\left(\dfrac{3}{4};1;\dfrac{9}{4}\right);\left(-\dfrac{3}{4};-1;-\dfrac{9}{4}\right)\right\}\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị thực của tham số a để biểu thức
B
log
3
(
2
-
a
)
có nghĩa
Đọc tiếp
Tìm tất cả các giá trị thực của tham số a để biểu thức B = log 3 ( 2 - a ) có nghĩa
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số a sao cho hàm số đạt cực trị tại thỏa mãn: . A. . B. . C. . D. .
Đọc tiếp
Tìm tất cả các giá trị thực của tham số a sao cho hàm số ![]() đạt cực trị tại
đạt cực trị tại ![]() thỏa mãn:
thỏa mãn: ![]() .
.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho các số tự nhiên 12,46,81,31
a, Tìm tất cả các ước thực sự của mỗi số
b, tì tổng của các ước thực sự của mỗi số