Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc - 2ac = abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là:
A. 14
B. 14
C. 1/ 14
D. Không tồn tại
Trong không gian Oxyz, cho ba điểm A(3;0;0),B(0;4;0),C(0;0;c) với c là số thực thay đổi khác 0. Khi c thay đổi thì trực tâm H của tam giác ABC luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A. 5 2
B. 5 4
C. 12 5
D. 6 5
Trong không gian Oxyz, cho ba điểm A (a;0;0) B (1;b;0) C (1;0;c) với a, b, c là các số thực thay đổi thỏa mãn H (3;2;1) là trực tâm của tam giác ABC. Tính S = a + b + c
\(\overrightarrow{AB}=\left(1-a;b;0\right);\overrightarrow{AC}=\left(1-a;0;c\right);\overrightarrow{HC}=\left(-2;-2;c-1\right);\overrightarrow{HB}=\left(-2;b-2;-1\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}.\overrightarrow{HC}=0\\\overrightarrow{AC}.\overrightarrow{HB}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-2\left(1-a\right)-2b=0\\-2\left(1-a\right)-c=0\end{matrix}\right.\) \(\Rightarrow c=2b=2\left(a-1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(bc;c\left(a-1\right);b\left(a-1\right)\right)=\left(2\left(a-1\right)^2;2\left(a-1\right)^2;\left(a-1\right)^2\right)=\left(a-1\right)^2.\left(2;2;1\right)\)
A;B;C;H đồng phẳng
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right].\overrightarrow{HB}=0\Rightarrow2.\left(-2\right)+2.\left(-2\right)+1.\left(c-1\right)=0\)
\(\Rightarrow c=9\Rightarrow b=\dfrac{9}{2}\Rightarrow a=\dfrac{11}{2}\)
Trong không gian Oxyz, cho ba điểm A(-10; -5;8), B(2;1;-1), C(2;3;0) và mặt phẳng (P): x+2y-2z-9=0. Xét M là điểm thay đổi trên (P) sao cho M A 2 + 2 M B 2 + 3 M C 2 đạt giá trị nhỏ nhất.Tính M A 2 + 2 M B 2 + 3 M C 2 .
A. 54
B. 282
C. 265
D. 328
Trong không gian Oxyz cho ba điểm A(-10;-5;8), B(2;1;-1), C(2;3;0) và mặt phẳng (P): x+2y-2z-9=0. Xét điểm M là điểm thay đổi trên (P) sao cho M A 2 + 2 M B 2 + 3 M C 2 đạt giá trị nhỏ nhất. Tính M A 2 + 2 M B 2 + 3 M C 2
A. 54
B. 282
C. 256
D. 328
Trong không gian Oxyz, cho ba điểm A - 1 ; 0 ; 0 , B 0 ; 2 ; 0 , C 0 ; 0 ; 3 . Gọi M là điểm thay đổi trên mặt phẳng (ABC) và N là điểm trên tia OM sao cho O M . O N = 12 . Biết luôn thuộc một mặt cầu cố định. Xác định tọa độ tâm mặt cầu đó.
A. 5
B. -1
C. -5
D. 4
Trong không gian Oxyz, cho ba điểm A - 1 ; 0 ; 0 , B 0 ; 2 ; 0 , C 0 ; 0 ; 3 . Gọi M là điểm thay đổi trên mặt phẳng (ABC) và N là điểm trên tia OM sao cho O M . O N = 12 . Biết luôn thuộc một mặt cầu cố định. Xác định tọa độ tâm mặt cầu đó.
A. (-1;2;3)
B. (12;6;4)
C. (-6;3;2)
D. (6;-3;-2)
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là những số thực dương thay đổi sao cho a 2 + 4 b 2 + 16 c 2 = 49 . Tính tổng F = a 2 + b 2 + c 2 sao cho khoảng cách từ O đến (ABC) là lớn nhất.
A. F = 51 5
B. F = 51 4
C. F = 49 5
D. F = 49 4
Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c khác 0
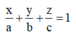
- Sử dụng bất đẳng thức
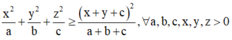
Đẳng thức xảy ra khi và chỉ khi
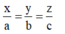
Cách giải:
![]()
Mặt phẳng (ABC) có phương trình:
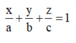
Khoảng cách từ O đến (ABC):
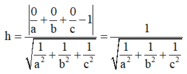
Ta có
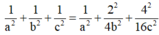
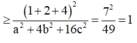
Dấu “=” xảy ra khi và chỉ khi:
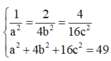
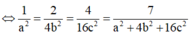
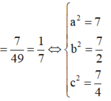
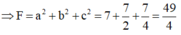
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là những số thực dương thay đổi sao cho a2 + 4b2 + 16c2 = 49. Tính tổng F = a2 + b2 +c2 sao cho khoảng cách từ O đến (ABC) là lớn nhất.
A. F = 51 5
B. F = 51 4
C. F = 49 5
D. F = 49 4
Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c khác 0): x a + y b + z c = 1
- Sử dụng bất đẳng thức: 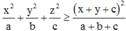
![]()
Đẳng thức xảy ra khi và chỉ khi x a = y b = z c
Cách giải:
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c > 0)
Mặt phẳng (ABC) có phương trình: x a + y b + z c = 1
Khoảng cách từ O đến (ABC):
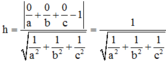
Ta có: 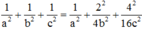
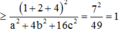
Dấu “=” xảy ra khi và chỉ khi:
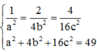
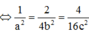
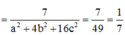
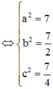
=> 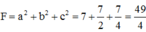
Trong không gian Oxyz, cho ba điểm A(a,0,0),B(0,b,0),C(0,0,c) với a,b,c là những số dương thay đổi sao cho a 2 + 4 b 2 + 16 c 2 = 49 .Tính tổng P = a 2 + b 2 + c 2 sao cho khoảng cách từ O đến mặt phẳng là lớn nhất.
A. P=49/4
B. P=49/5
C. P=51/4
D. P=51/5