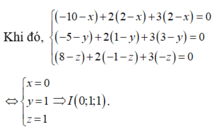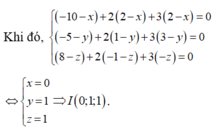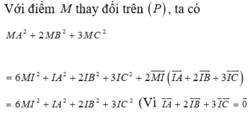Các câu hỏi tương tự
Trong không gian Oxyz cho ba điểm A(-10;-5;8), B(2;1;-1), C(2;3;0) và mặt phẳng (P): x+2y-2z-90. Xét điểm M là điểm thay đổi trên (P) sao cho
M
A
2
+
2
M
B
2
+
3
M
C
2
đạt giá trị nhỏ nhất. Tính
M
A
2
+
2
M
B
2
+...
Đọc tiếp
Trong không gian Oxyz cho ba điểm A(-10;-5;8), B(2;1;-1), C(2;3;0) và mặt phẳng (P): x+2y-2z-9=0. Xét điểm M là điểm thay đổi trên (P) sao cho M A 2 + 2 M B 2 + 3 M C 2 đạt giá trị nhỏ nhất. Tính M A 2 + 2 M B 2 + 3 M C 2
A. 54
B. 282
C. 256
D. 328
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; -2; -1), B (-2,-4,3), C (1;3;-1) và mặt phẳng (P): x + y -2z – 3 0. Tìm điểm M ∈ (P) sao cho
M
A
→
+
M
B
→
+
2
M
C...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; -2; -1), B (-2,-4,3), C (1;3;-1) và mặt phẳng (P): x + y -2z – 3 = 0. Tìm điểm M ∈ (P) sao cho M A → + M B → + 2 M C → đạt giá trị nhỏ nhất.
A . M 1 2 ; 1 2 ; - 1
B . M - 1 2 ; - 1 2 ; 1
C . M 2 ; 2 ; - 4
D . M - 2 ; - 2 ; 4
Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-30. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c. A. -3 B. -2 C. 2 D. 3
Đọc tiếp
Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-3=0. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c.
A. -3
B. -2
C. 2
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0;-2;-l), B(-2;-4;3), C(l;3;-l) và mặt phẳng (P): x+y-2z-30 . Tìm điểm
M
∈
(
P
)
sao cho
|
M
A
+
M
B
⇀
+
2
M
C
⇀
|
đạt giá trị nhỏ nhất.
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0;-2;-l), B(-2;-4;3), C(l;3;-l) và mặt phẳng (P): x+y-2z-3=0 . Tìm điểm M ∈ ( P ) sao cho | M A + M B ⇀ + 2 M C ⇀ | đạt giá trị nhỏ nhất.
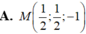

![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;4;5), B(3;4;0), C(2;-1;0) và mặt phẳng (P): 3x+3y-2z-290. Gọi M(a,b,c) là điểm thuộc (P) sao cho
M
A
→
2
+
M
B
→
2
+
3
M
C
→...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;4;5), B(3;4;0), C(2;-1;0) và mặt phẳng (P): 3x+3y-2z-29=0. Gọi M(a,b,c) là điểm thuộc (P) sao cho M A → 2 + M B → 2 + 3 M C → 2 đạt giá trị nhỏ nhất. Tính tổng a+b+c.
A. 8
B. 10
C. -10
D. -8
Trong không gian Oxyz cho ba điểm A (0;2;-2), B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc mặt phẳng (
α
): 2x -y +2z + 7 0 sao cho biểu thức
3
M
A
→
+
5
M
C
→
-
7
M
C...
Đọc tiếp
Trong không gian Oxyz cho ba điểm A (0;2;-2),
B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc
mặt phẳng ( α ): 2x -y +2z + 7 = 0 sao cho biểu
thức 3 M A → + 5 M C → - 7 M C → đạt giá trị nhỏ nhất.
Tính a+b+c
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;2), B(2;-2;1),C(-2;0;1) và mặt phẳng
(
P
)
:
2
x
+
2
y
+
z
-
3
0
.Tọa độ điểm M thuộc mặt phẳng (P) sao cho M cách đều ba điểm A, B, C là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;2), B(2;-2;1),C(-2;0;1) và mặt phẳng ( P ) : 2 x + 2 y + z - 3 = 0 .Tọa độ điểm M thuộc mặt phẳng (P) sao cho M cách đều ba điểm A, B, C là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;2), B(2;-2;1), C(-2;0;1) và mặt phẳng (P): 2x+2y+z-30. Tọa độ điểm M thuộc mặt phẳng (P) sao cho M cách đều ba điểm A, B, C là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;2), B(2;-2;1), C(-2;0;1) và mặt phẳng (P): 2x+2y+z-3=0. Tọa độ điểm M thuộc mặt phẳng (P) sao cho M cách đều ba điểm A, B, C là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;4;5), B(3;4;0), C(2;-1;0) và mặt phẳng (P):3x-3y-2z-120. Gọi thuộc M(a;b;c) sao cho
M
A
2
+
M
B
2
+
M
C
2
đạt giá trị nhỏ nhất. Tính tổng a+b+c. A. 3. B. 2. C. –2. D. –3.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;4;5), B(3;4;0), C(2;-1;0) và mặt phẳng (P):3x-3y-2z-12=0. Gọi thuộc M(a;b;c) sao cho M A 2 + M B 2 + M C 2 đạt giá trị nhỏ nhất. Tính tổng a+b+c.
A. 3.
B. 2.
C. –2.
D. –3.