Chọn D
Gọi G (2;2;-2) là trọng tâm tam giác ABC, khi đó ![]()
Ta có:
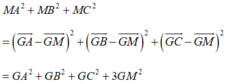
đạt giá trị nhỏ nhất khi M là hình chiếu vuông góc của G trên mặt phẳng (P). Khi đó tọa độ của M (a;b;c) và vecto ![]() cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ
cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ 
Vậy a+b+c=3.
Chọn D
Gọi G (2;2;-2) là trọng tâm tam giác ABC, khi đó ![]()
Ta có:
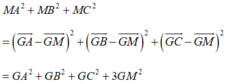
đạt giá trị nhỏ nhất khi M là hình chiếu vuông góc của G trên mặt phẳng (P). Khi đó tọa độ của M (a;b;c) và vecto ![]() cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ
cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ 
Vậy a+b+c=3.
Trong không gian Oxyz cho ba điểm A (0;2;-2),
B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc
mặt phẳng ( α ): 2x -y +2z + 7 = 0 sao cho biểu
thức 3 M A → + 5 M C → - 7 M C → đạt giá trị nhỏ nhất.
Tính a+b+c
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt phẳng (P): 3x-3y+2z+37=0 và các điểm A(4;1;5), B(3;0;1), C(-1;2;0). Biết rằng có điểm M(a;b;c) thuộc mặt phẳng (P) để biểu thức M A → . M B → + M B → . M C → + M C → . M A → đạt giá trị nhỏ nhất. Biểu thức a 2 + b 2 - c 2 có giá trị là
A. 69
B. 61
C. 18
D. 22
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1;2; –3), B(–1;1;2), C(0;–3;–5). Xác định điểm M trên mặt phẳng Oxy sao cho: M A → + M B → + M C → đạt giá trị nhỏ nhất. Giá trị nhỏ nhất đó là
A. 0
B. 5
C. 5
D. 6
Trong không gian Oxyz cho A(1;-1;2), B(-2;0;3), C(0;1;-2). M(a;b;c) là điểm thuộc mặt phẳng (Oxy) sao cho biểu thức S = M A → . M B → + 2 M B → . M C → + 3 M C → . M A → đạt giá trị nhỏ nhất. Khi đó T = 12 a + 12 b + c có giá trị là
A. T = -1
B. T = 3
C. T = -3
D. T = 1
Trong không gian Oxyz, cho A(1;-1;2),B(-2;0;3),C(0;1;-2). Gọi M(a;b;c) là điểm thuộc mặt phẳng (Oxy) sao cho biểu thức S = M A → . M B → + 2 M B → . M C → + 3 M C → . M A → đạt giá trị nhỏ nhất. Khi đó T=12a+12b+c có giá trị là
A. T=3
B. T=-3
C. T=1
D. T=-1
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x - y + z + 3 = 0 và ba điểm A(0;1;2), B(1;1;1), C(2;-2;3) Tọa độ điểm M thuộc (P) sao cho M A → + M B → + M C → nhỏ nhất là
A. M(0;0;−3)
B. M(1;1;−3)
C. M(−1;2;0)
D. M(2;1;−1)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + z -1 = 0 và điểm A (0; -2; 3), B (2; 0; 1). Điểm M (a; b; c) thuộc (P) sao cho MA + MB nhỏ nhất.
Giá trị của a2 + b2 + c2 bằng:
A. 41/4
B. 9/4
C. 7/4
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; -2; -1), B (-2,-4,3), C (1;3;-1) và mặt phẳng (P): x + y -2z – 3 = 0. Tìm điểm M ∈ (P) sao cho M A → + M B → + 2 M C → đạt giá trị nhỏ nhất.
A . M 1 2 ; 1 2 ; - 1
B . M - 1 2 ; - 1 2 ; 1
C . M 2 ; 2 ; - 4
D . M - 2 ; - 2 ; 4
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0;-2;-l), B(-2;-4;3), C(l;3;-l) và mặt phẳng (P): x+y-2z-3=0 . Tìm điểm M ∈ ( P ) sao cho | M A + M B ⇀ + 2 M C ⇀ | đạt giá trị nhỏ nhất.
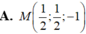

![]()
![]()