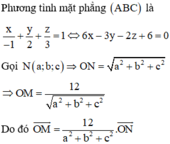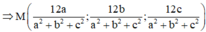Các câu hỏi tương tự
Trong không gian Oxyz, cho ba điểm
A
-
1
;
0
;
0
,
B
0
;
2
;
0
,
C
0
;
0
;
3
. Gọi M là điểm thay đổ...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A - 1 ; 0 ; 0 , B 0 ; 2 ; 0 , C 0 ; 0 ; 3 . Gọi M là điểm thay đổi trên mặt phẳng (ABC) và N là điểm trên tia OM sao cho O M . O N = 12 . Biết luôn thuộc một mặt cầu cố định. Xác định tọa độ tâm mặt cầu đó.
A. 5
B. -1
C. -5
D. 4
Trong không gian vưới hệ tọa độ Oxyz cho các điểm A(1;0;0), B(0;2;0), C(0;0;3). Gọi M là một điểm thay đổi nằm trên mặt phẳng (ABC), N là điểm nằm trên OM sao cho OM.ON 12. Biết rằng khi M thay đổi, điểm N luôn nằm trên một mặt cầu cố định. Tính bán kính R của mặt cầu đó A. 4 B. 6 C. 5 D. 7
Đọc tiếp
Trong không gian vưới hệ tọa độ Oxyz cho các điểm A(1;0;0), B(0;2;0), C(0;0;3). Gọi M là một điểm thay đổi nằm trên mặt phẳng (ABC), N là điểm nằm trên OM sao cho OM.ON = 12. Biết rằng khi M thay đổi, điểm N luôn nằm trên một mặt cầu cố định. Tính bán kính R của mặt cầu đó
A. 4
B. 6
C. 5
D. 7
Trong không gian với hệ tọa độ Oxyz, xét các điểm
A
0
;
0
;
1
,
B
m
;
0
;
0
,
C
0
;
n
;
0
,
D...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, xét các điểm A 0 ; 0 ; 1 , B m ; 0 ; 0 , C 0 ; n ; 0 , D 1 ; 1 ; 1 với m > 0, n > 0 và m + n = 1 . Biết rằng khi m, n thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng (ABC) và đi qua D. Tính bán kính R của mặt cầu đó.
A. R = 1
B. R = 2 2
C. R = 3 2
D. R = 3 2
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P). A. 2017 B.
2014
3
C.
2016
3
D.
2015...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(a; 0; 0), B(0; b; 0), C(0; 0; c) với a, b, c dương. Biết A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c = 2. Biết rằng khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(2016; 0; 0) tới mặt phẳng (P).
A. 2017
B. 2014 3
C. 2016 3
D. 2015 3
Trong không gian với hệ tọa độ Oxyz, xét các điểm
A
a
;
0
;
0
,
B
0
;
b
;
0
,
C
0
;
0
;
c
với a, b, c khác 0 và
a...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, xét các điểm A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c với a, b, c khác 0 và a + 2 b + 2 c = 6 . Biết rằng khi a, b, c thay đổi thì quỹ tích tâm mặt cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ điểm O đến mặt phẳng (P)
A. d = 1
B. d = 3
C. d = 2
D. d = 3
Trong không gian với hệ tọa độ Oxyz cho hai điểm M(1;2;3), N(3;4;5) và mặt phẳng
P
:
x
+
2
y
+
3
z
-
14
0
. Gọi
∆
là đường thẳng thay đổi nằm trong mặt phẳng (P). Gọi H, K lần lượt là hình chiếu vuông góc của M, N trên
∆
. Biết rằng khi
M
H
N
K
thì trung điểm của HK luôn thuộc...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm M(1;2;3), N(3;4;5) và mặt phẳng P : x + 2 y + 3 z - 14 = 0 . Gọi ∆ là đường thẳng thay đổi nằm trong mặt phẳng (P). Gọi H, K lần lượt là hình chiếu vuông góc của M, N trên ∆ . Biết rằng khi M H = N K thì trung điểm của HK luôn thuộc một đường thẳng d cố định, phương trình của đường thẳng d là
A. x = 1 y = 13 - 2 t z = - 4 + t
B. x = t y = 13 - 2 t z = - 4 + t
C. x = t y = 13 + 2 t z = - 4 + t
D. x = t y = 13 - 2 t z = - 4 - t
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;2;3), B(3;4;5) và mặt phẳng
(
α
)
:x+2y+3z-140. Gọi
Δ
là đường thẳng thay đổi nằm trong mặt phẳng
(
α
)
, các điểm M,N lần lượt là hình chiếu vuông góc của A,B trên
Δ
. Biết rằng khi AM BN thì trung điểm của MN luôn thuộc một đường thẳng cố định. Viết phương trình đường thẳng cố định đó. A.
x...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;2;3), B(3;4;5) và mặt phẳng ( α ) :x+2y+3z-14=0. Gọi Δ là đường thẳng thay đổi nằm trong mặt phẳng ( α ) , các điểm M,N lần lượt là hình chiếu vuông góc của A,B trên Δ . Biết rằng khi AM = BN thì trung điểm của MN luôn thuộc một đường thẳng cố định. Viết phương trình đường thẳng cố định đó.
A. x = 4 + t y = 5 - 2 t z = 1 + t
B. x = 5 + t y = 3 - 2 t z = 1 + t
C. x = 2 + t y = 1 - 2 t z = 3 + t
D. x = 4 + t y = 5 + 2 t z = t
Trong không gian với hệ tọa độ Oxyz, cho A(a;0;0), B(0;b;0), C(0;0;c) và a, b, c dương. Biết rằng khi A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c 2018 và khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC luôn thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(1;0;0) tới mặt phẳng (P).
A
.
168
3
B
.
336
3
C
....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(a;0;0), B(0;b;0), C(0;0;c) và a, b, c dương. Biết rằng khi A, B, C di động trên các tia Ox, Oy, Oz sao cho a + b + c = 2018 và khi a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC luôn thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M(1;0;0) tới mặt phẳng (P).
A . 168 3
B . 336 3
C . 1009 3
D . 2018 3
Trong không gian với hệ toạ độ Oxyz, xét các điểm
A
a
;
0
;
0
,
B
0
;
b
;
0
,
C
0
;
0
;
c
, với abc 0 và...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, xét các điểm A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c , với abc > 0 và a + 2 b + 2 c = 6 . Biết rằng khi a, b, c thay đổi thì quỹ tích tâm mặt cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ điểm O tới mặt phẳng (P)
A. 1
B. 3
C. 2
D. 3