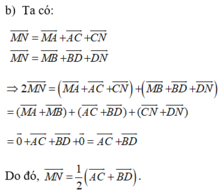Cho tứ diện ABCD. Gọi M, N là trung điểm AB, CD; P,Q là hai điểm theo thứ tự thuộc hai cạnh AC, BD sao cho PA/PC=QB/QD. Chứng minh rằng M, N, P, Q cùng thuộc một mặt phẳng.

Những câu hỏi liên quan
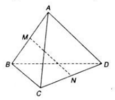
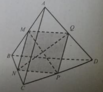
Cho hình tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện đi qua ba điểm M, N, P là:
A. hình thang
B. hình bình hành
C. hình thoi
D. hình chữ nhật
Gọi Q là trung điểm AD chứng mình MNPQ là hình bình hành ⇒ M, N, P, Q cùng thuộc một mặt phẳng ⇒ thiết diện là hình bình hành.
Đúng 0
Bình luận (0)
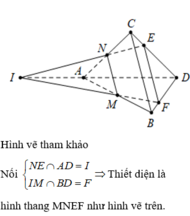
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB, AC; điểm E trên cạnh CD sao cho
E
D
3
E
C
. Thiết diện tạo bởi mặt phẳng
M
N
E
và tứ diện ABCD là: A. Tam giác MNE B. Tứ giác MNEF với F là điểm bất kỳ trên cạnh BD C. Hình bình hành MNEF với F là điểm trên cạnh BD với EF//BC D. Hình thang MNEF với F là điểm trên cạnh BD sao cho EF//BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB, AC; điểm E trên cạnh CD sao cho E D = 3 E C . Thiết diện tạo bởi mặt phẳng M N E và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEF với F là điểm bất kỳ trên cạnh BD
C. Hình bình hành MNEF với F là điểm trên cạnh BD với EF//BC
D. Hình thang MNEF với F là điểm trên cạnh BD sao cho EF//BC
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là: A. Tam giác MNE B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD
C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC
D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đáp án C
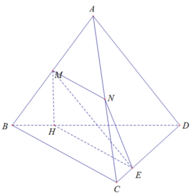
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang
Đúng 0
Bình luận (0)
Cho hình tứ diện ABCD. Gọi M và N lần lượt là các trung điểm của AB và CD.
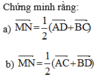
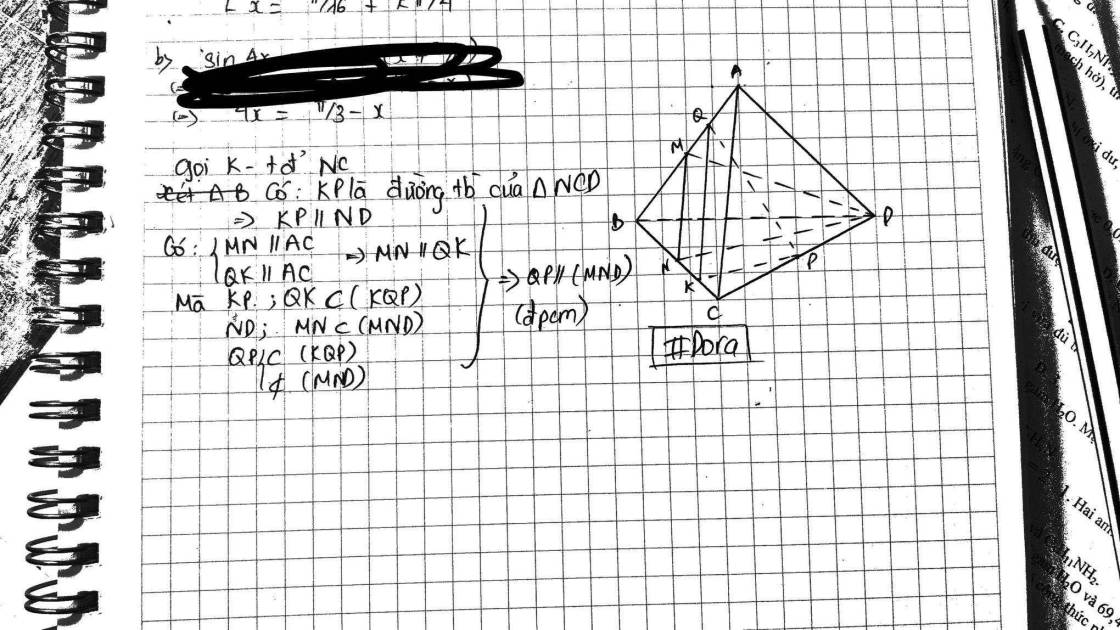
Cho tứ diện ABCD. Gọi M,N,P,Q lần lượt là trung điểm các đoạn AB,BC,CD,AM. CMR: PQ // (MND)
cho tứ diện abcd. gọi m, n lần lượt là trung điểm bc, cd. p là điểm bất kì thuộc cạnh ab. xác định giao tuyến của mặt phẳng (mnp) và các mặt của tứ diện
Đọc tiếp
cho tứ diện abcd. gọi m, n lần lượt là trung điểm bc, cd. p là điểm bất kì thuộc cạnh ab. xác định giao tuyến của mặt phẳng (mnp) và các mặt của tứ diện
Cho tứ diện ABCD có AB AC AD; góc BAC bằng góc BAD bằng
60
o
. Gọi M và N là trung điểm của AB và CDGóc giữa
A
B
→
và
C
D
→
bằng: A.
30
o
B.
60
o
C.
90
o...
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60 o . Gọi M và N là trung điểm của AB và CD
Góc giữa A B → và C D → bằng:
A. 30 o
B. 60 o
C. 90 o
D. 120 o
Ta có: A B → . C D → = A B → A D → − A C → = A B → . A D → − A B → . A C →
= A B → . A D → . cos B A D − A B → . A C → cos B A C
= A B 2 . cos 60 ° − A B 2 cos 60 ° (do AB = AC = AD và B A C ^ = B A D ^ = 60 ° )
= 0
Suy ra A B ⊥ C D hay góc giữa hai vecto A B → và C D → là 90 ° .
ĐÁP ÁN C
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD (AB//CD) và \(\widehat{D}\) = 45 độ. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Tính diện tích các tứ giác ABCD, MNPQ nếu AB = 2cm, CD = 6cm.
b) Tính tỉ số diện tích các tứ giác ABCD, MNPQ nếu các dữ liệu về góc D, cạnh AB, CD không nhất thiết phải như đề cho trên.
Cho hình thang ABCD ( AB // CD) có diện tích là S, Cd = 3/2AB. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Tính diện tích tứ giác EMFN theo S
Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của BC và AD. Biết
A
B
C
D
a
,
M
N
a
3
2
. Tính góc giữa hai đường thẳng AB và CD. A.
45
°
B.
30
°
C.
60
°
D.
90
°
Đọc tiếp
Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của BC và AD.
Biết A B = C D = a , M N = a 3 2 . Tính góc giữa hai đường thẳng AB và CD.
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Đáp án C
Gọi P là trung điểm của AC.
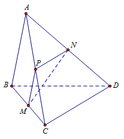
Ta có: P N / / C D , M P / / A B ⇒ A B ; C D = M P ; P N
P N = M P = a 2 , M N = a 3 2 ⇒ cos M P N ⏜ = − 1 2 ⇒ M P N ⏜ = 120 °
⇒ A B ; C D ⏜ = 60 °
Đúng 0
Bình luận (0)