Đáp án C
Gọi P là trung điểm của AC.
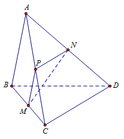
Ta có: P N / / C D , M P / / A B ⇒ A B ; C D = M P ; P N
P N = M P = a 2 , M N = a 3 2 ⇒ cos M P N ⏜ = − 1 2 ⇒ M P N ⏜ = 120 °
⇒ A B ; C D ⏜ = 60 °
Đáp án C
Gọi P là trung điểm của AC.

Ta có: P N / / C D , M P / / A B ⇒ A B ; C D = M P ; P N
P N = M P = a 2 , M N = a 3 2 ⇒ cos M P N ⏜ = − 1 2 ⇒ M P N ⏜ = 120 °
⇒ A B ; C D ⏜ = 60 °
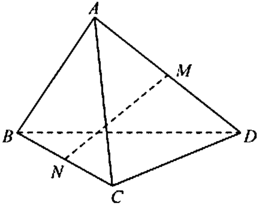
Cho tứ diện ABCD có AB = CD = a. Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30 ° .
A. M N = a 2
B. M N = a 3 2
C. M N = a 3 3
D. M N = a 4
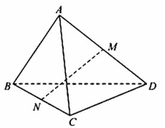
Cho tứ diện ABCD có A B = C D = a . Gọi M và N lần lượt là trung điểm của AD và BC. Xác định độ dài đoạn thẳng MN để góc giữa hai đường thẳng AB và MN bằng 30 ° .
A. M N = a 2
B. M N = a 3 2
C. M N = a 3 3
D. M N = a 4
Cho tứ diện ABCD có A B = C D = 2 a . Gọi M, N lần lượt là trung điểm của BC, AD và M N = a 3 . Tính góc tạo bởi hai đường thẳng AB và CD
A. 30 °
B. 45 °
C. 60 °
D. 90 °
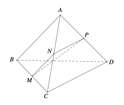
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CA và AD (tham khảo hình vẽ bên). Biết M N P ^ = 150 0 . Góc giữa hai đường thẳng AB và CD là
A. 30 °
B. 45 °
C. 90 °
D. 60 °
Cho hình chóp S.ABCD có đáy là hình thang vuông tại B. AB=BC=a, AD=2a. Biết SA vuông góc với đáy (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm SB,CD. Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC)
A. 5 5
B. 55 10
C. 3 5 10
D. 2 5 5
Cho tứ diện đều ABCD cạnh AB=1. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, AD. Tính khoảng cách giữa hai đường thẳng CM và NP.
A. 10 10
B. 10 20
C. 3 10 10
D. 3 10 20
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a tâm O. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng 60 ° . Tính cosin góc giữa đường thẳng và mặt phẳng (SBD)
A. 41 41
B. 5 5
C. 2 5 5
D. 2 41 41
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA vuông góc với mặt đáy (ABCD), SA = a. Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa đường thẳng MN và (SAC)
A. 2 5
B. 55 10
C. 3 5 10
D. 1 5
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai đường thẳng MG và NP. Khi đó cosα bằng
A. 2 6
B. 2 4
C. 3 6
D. 3 4