hình thang cân MNPQ có đường chéo cắt nhau tại O Chứng minh OM=ON; OP=OQ giúp mình với

Những câu hỏi liên quan
Mọi người giải giúp mk vs ạ : Cho hình thoi ABCD có 2 đường chéo AC và BD cắt nhau tại O. Qua O kẻ OM,ON,OP,OQ vuông vóc với AB,BC,CD,DA lần lượt tại M,N,P,Q. a) chứng minh OM=ON=OP=OQ. b) Chứng minh 3 điểm M,O,P thẳng hàng. c) Tứ giác MNPQ là hình gì? Vì sao?
cho hình thang MNPQ ( MN là đáy nhỏ) hai đường chéo MP và NQ cắt nhau tại O. Biết NMP=MNQ , qua O vẽ đường thẳng EF // PQ (E thuộc MQ, F thuộc NP) chứng minh NMQP, FEQP , MNFE là hình thang cân
ta có MNPQ là hình thang=>MN//PQ
mà \(=\angle\left(NMP\right)=\angle\left(MNQ\right)=>\angle\left(NQP\right)=\angle\left(MPQ\right)\)
=>tam giác MNO cân tại O=>MO=NO
=>tam giác QOP cân tại O=>OQ=Op
=>MO+OP=NO+OQ=>NQ=MP
=>MNPQ là hình thang cân
\(=>\angle\left(M\right)=\angle\left(N\right)\left(1\right)\)
\(\angle\left(Q\right)=\angle\left(P\right)\left(2\right)\)
mà EF//PQ=>EF//MN
=>MNFE là hình thang(3)
từ (1)(3)=>MNFE là hình thang cân
=>EFPQ là hình thang(4)
(2)(4)=>EFPQ là hình thang cân
Đúng 2
Bình luận (0)
Ta có: \(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{ONM}=\widehat{OQP}\)
mà \(\widehat{OMN}=\widehat{ONM}\)
nên \(\widehat{OPQ}=\widehat{OQP}\)
Xét ΔOMN có \(\widehat{OMN}=\widehat{ONM}\)
nên ΔOMN cân tại O
Xét ΔOPQ có \(\widehat{OPQ}=\widehat{OQP}\)
nên ΔOPQ cân tại O
Ta có: OM+OP=MP
ON+OQ=QN
mà OM=ON
và OP=OQ
nên MP=QN
Hình thang MNPQ có MP=QN
nên MNPQ là hình thang cân
Suy ra: \(\widehat{EMN}=\widehat{FNM}\) và \(\widehat{EQP}=\widehat{FPQ}\)
Hình thang EMNF có \(\widehat{EMN}=\widehat{FNM}\)
nên EMNF là hình thang cân
Hình thang EQPF có \(\widehat{EQP}=\widehat{FPQ}\)
nên EQPF là hình thang cân
Đúng 1
Bình luận (0)
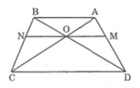
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
Trong ΔDAB, ta có: OM // AB (gt)
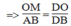 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)
Trong ΔCAB, ta có: ON // AB (gt)
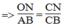 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)
Trong ΔBCD, ta có: ON // CD (gt)
Suy ra: ![]() (định lí Ta-lét) (3)
(định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra: 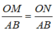
Vậy: OM = ON
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD); hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt tại M và N. Chứng minh OM = ON
Ta có: MN // AB (gt); AB // CD(gt) => MN // AB // CD
Xét tam giác ABC có: OM // AB (MN // AB)
=> \(\dfrac{OM}{AB}=\dfrac{CM}{CA}\) (hệ quả định lý Ta lét trong tam giác) (1)
Xét tam giác ABD có: ON // AB (MN // AB)
=> \(\dfrac{ON}{AB}=\dfrac{DN}{DB}\) (hệ quả định lý Ta lét trong tam giác) (2)
Xét hình thang ABCD có: MN // AB // CD (cmt)
=> \(\dfrac{CM}{CA}=\dfrac{DN}{DB}\) (định lý Ta lét trong hình thang) (3)
Từ (1) (2) (3) => OM = ON
Đúng 4
Bình luận (1)
Trong ∆DAB có: \(\dfrac{MO}{AB}=\dfrac{DO}{DB}\) ( hệ quả Ta lét) (1)
Trong ∆CAB có: \(\dfrac{NO}{AB}=\dfrac{CO}{AC}\) ( hệ quả Ta lét) (2)
Trong ∆OAB có: \(\dfrac{CO}{CA}=\dfrac{DO}{DB}\) ( hệ quả Ta lét) (3)
từ (1), (2), (3) => \(\dfrac{MO}{AB}=\dfrac{NO}{AB}\) =>\(MO=NO\)
Đúng 2
Bình luận (1)
cho hình thang cân MNPQ có đáy nhỏ MN và hai đường chéo cắt nhau tại B và hai cạnh bên cắt nhau tại A
a) chứng minh tam giác AMN cân
b) chứng minh AB là trung trực của MN và PQ
a) Ta có: góc Q =góc P
=> AQ = AP ( quan hệ giữa góc và cạnh đối diện)
Ta có: AM + MQ = AQ
AN + NP = AP
Mà MQ = NP ( MNPQ là hình thang cân).
AQ = AP (cmt)
=> AM = AN => tam giác MAN cân tại A.
Câu b bạn tự làm nha
Đúng 0
Bình luận (0)
Bài 7 (2) :Cho hình thang ABCD (AB//CD) ; hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với AB cắt AD lần lượt tại M và N . Chứng minh OM = ON
Bài 1: Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N.
1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N. 1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
cho hình thang MNPQ đường chéo cắt nhau tại O a) chứng minh OM.OQ=ON.OP b) đường tg đi qua O cắt MQ và NP thứ tự ại A và B chứng minh OA=OB
a: Xét ΔOMN và ΔOPQ có
\(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{MON}=\widehat{POQ}\)
Do đó; ΔOMN\(\sim\)ΔOPQ
Suy ra: OM/OP=ON/OQ
hay \(OM\cdot OQ=ON\cdot OP\)
b: Xét ΔMQP có AO//QP
nên AO/PQ=MA/MQ(1)
Xét ΔNQP có OB//QP
nên OB/PQ=NB/NP(2)
Xét hình thang MNPQ có AB//QP
nên MA/MQ=NB/NP(3)
Từ (1), (2) và (3) suy ra OA=OB
Đúng 0
Bình luận (0)






















