Bạn viết lại đề bài đi mik đọc không hiểu

a: Xét ΔABH và ΔACH có

AB=AC

AH chung

HB=HC

=>ΔABH=ΔACH

b: Xét ΔACB có

BM,AH là trung tuyến

BM cắt AH tại G

=>G là trọng tâm

=>C,G,N thẳng hàng

c: Xét ΔABG và ΔACG có

AB=AC

góc BAG=góc CAG

AG chung

=>ΔABG=ΔACG

Tham khảo:

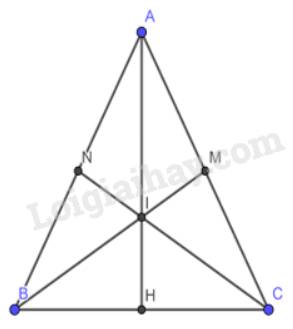
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.

Vì AB = AC (tính chất tam giác cân)

\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)

Xét tam giác AMB và tam giác ANC ta có :

AM = AN (cmt)

AB = AC

Góc A chung

\( \Rightarrow \Delta AMB =\Delta ANC\)

\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )

b) Vì BM và CN là các đường trung tuyến

Mà I là giao điểm của BM và CN

\( \Rightarrow \) I là trọng tâm của tam giác ABC

\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC

\( \Rightarrow \) H là trung điểm của BC

Này bạn oi trên tia đối của CA mà

b: Xét tứ giác ABCE có

M là trung điểm chung của AC và BE

=>ABCE là hình bình hành

=>CE//AB

c: Xét ΔHAB vuông tại H và ΔHKC vuông tại H có

HB=HC

góc HAB=góc HKC

=>ΔHAB=ΔHKC

=>HA=HK

Xét tứ giác ABKC có

H là trung điểm chung của BC và AK

AB=AC

=>ABKC là hình thoi

=>AC=CK

Xét ΔABC có

BM,AH là trung tuyến

BM cắt AH tại G

=>G là trọng tâm

=>3GH=AH

3GH+HC=AH+HC>AC=CK

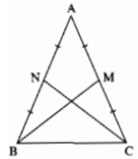
+) Do M là trung điểm của AC nên: 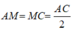 (1)

+) Do N là trung điểm của AB nên: 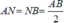 (2)

Lại có: AB = AC ( vì tam giác ABC cân tại A). (3)

Từ (1); (2); (3) suy ra: AN = NB = AM = MC.

+) Xét ∆ AMB và ∆ANC có:

Góc A chung

AM = AN ( chứng minh trên)

AB = AC ( vì tam giác ABC cân tại A)

Suy ra: ∆ AMB = ∆ANC ( c.g.c)

Do đó: BM = CN ( hai cạnh tương ứng).

Bạn tự vẽ hình nhé, lười quá :)

Xét tam giác ABC cân tại A (đề)

=> Góc ABC = góc ACB 

Ta có: M là trung điểm AC (gt)

           N là trung điểm AB (gt)

=> MN là đường trung bình tam giác ABC

=> MN // BC

Xét tứ giác NMBC có MN // BC và góc ABC = góc ACB (cmt)

=> Tứ giác NMBC là hình thang cân

=> BM = CN (2 đường chéo bằng nhau)

Vì M là trung điểm của AC,N là trung điểm của AB suy ra MN là đường trung bình của tam giác ABC suy ra MN//BC suy ra MNBC là hình thang

Vì tam giác ABC cân tại A suy ra B= C

Hinh thang MNBC có 2 góc kề 1 đáy bằng nhau suy ra MNBC là hình thang cân suy ra BM=CN 

                                                                         Chứng minh

Vì \(\Delta\)ABC cân tại A nên

=> AB =AC (1)

Mà NA = NB (N là trung điểm của AB) (2)

     MA = MC (M là trung điểm của AC) (3)

Từ (1), (2), (3) => NB = MC

Do \(\Delta\)ABC cân tại A nên góc B = góc C

Xét \(\Delta\)NBC và \(\Delta\)MCB có:

BC là cạnh chung

góc B = góc C (cmt)

NB = MC (cmt)

=> \(\Delta\)NBC = \(\Delta\)MCB (c.g.c)

=> BM = CN (2 cạnh tương ứng)

Vậy BM = CN

Xét tam giác ABM và ACN 

A la goc chung 

AB=AC

AN=AM( deu la trung diem cua 2 canh bang nhau

=>Tam giac ABM=ACN=> BM=CN(dpcm)

EM MS CÓ LỚP 5 THÔI Ạ !

xét tam giác ABM và ACN

A là góc chung 

AB = AC

AN = AM ( đều là trung điểm của hai cạnh bằng nhau 

= > Tam giác ABM=ACN=> BM= CN

chào em là thuthao ,em  có một câu hỏi , em mới học lớp năm

Ta có hình vẽ:

Theo bài ra ta có:

Tam giác ABC cân tại A

=> AB=AC ( hai cạnh bên của tam giác cân )

Ta lại có:

M là trung điểm của AC;N là trung điểm của AB

=> AN=BN=CM=AM

Ta có: \(\Delta ABM=\Delta ACN\) (c.g.c)

=> BM=CN ( hai cạnh tuơng ứng )

(đ.p.c.m)