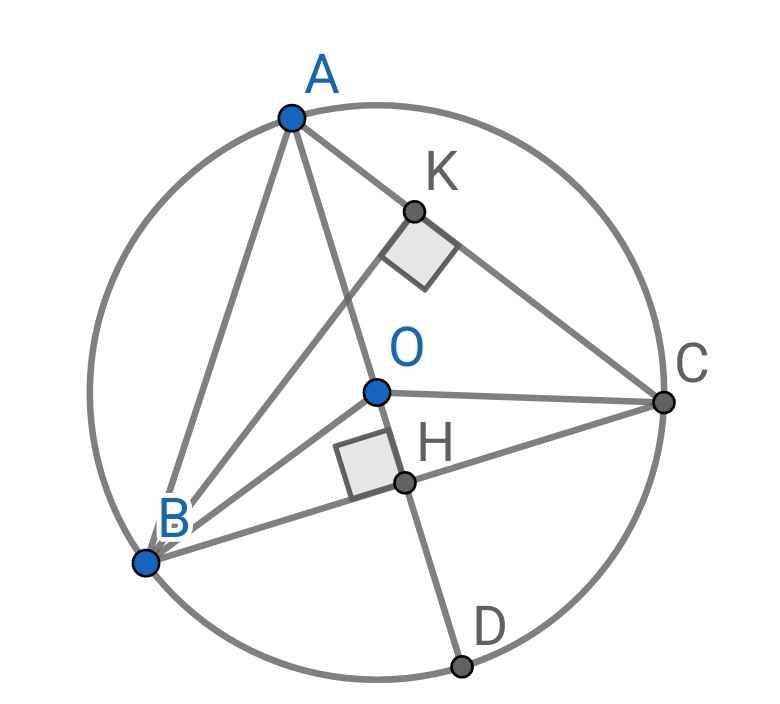
1.Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O; Gọi D là trung điểm AB, E là trọng tam của tam giác ACD. Chứng Minh OE vuông góc với CD
2. Cho tam giác ABC vuông tại AH=z, HB=x , HC=y. Chứng minh rằng nếu: x+y+x= xyz. thì \(z\ge\sqrt{3}\)
3.Cho các số dương a,b,c có tổng a+b+c = m không đổi; tìm a, b, c sao cho tổng B= ab+bc+ca lớn nhất.