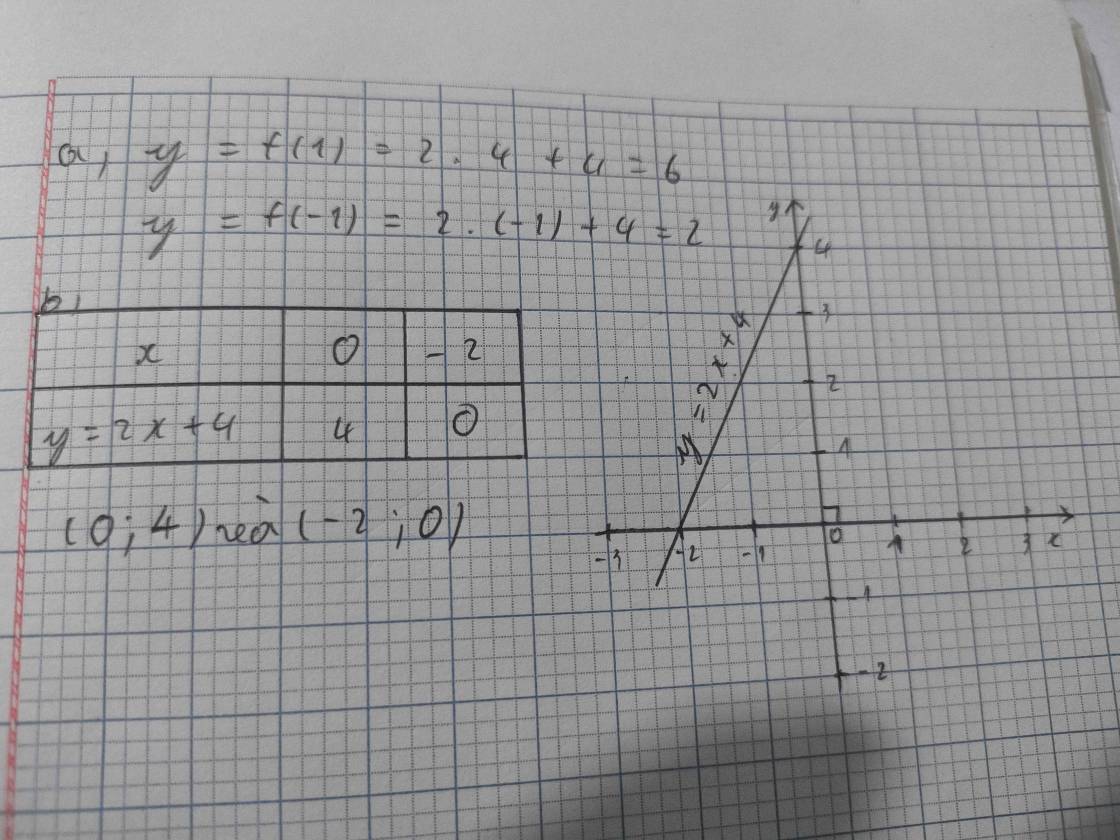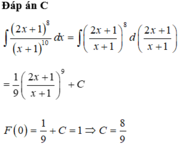cho hàm số f(x)=2x+1; G(x)=1-2x
a) tính f(g(x)) và g(f(x))
b) tìm x sao cho f(x)=g(x)

Những câu hỏi liên quan
Bải 1: Tìm tập xác định của các hàm số
sau:
a)
3x-2
2x+1
c) y=\sqrt{2x+1}-\sqrt{3-x}
b) y=
²+2x-3
d) y=
√2x+1
X
f(x)
Chú ý: * Hàm số cho dạng v
thi f(x) * 0.
ở Hàm số cho dạng y = v/(x) thì f(r) 2 0.
X
* Hàm số cho dạng " J7(p) thi f(x)>0.
a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)
Đúng 0
Bình luận (0)
Cho hàm số y f(x) 2x + 4a, Tính giá trị của hàm số: f(1) ; f(-1)b, Vẽ đồ thị hàm số: y 2x + 4
Đọc tiếp
Cho hàm số y= f(x) = 2x + 4
a, Tính giá trị của hàm số: f(1) ; f(-1)
b, Vẽ đồ thị hàm số: y = 2x + 4
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x + 1 ) ( 1 - 2 x ) 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 3
B. 1
C. 5
D. 2
Cho hàm số f(x) có đồ thị của hàm số yf’(x) như hình vẽ:Hàm số
y
f
(
2
x
-
1
)
+
x
3
3
+
x
2
-
2
x
nghịch biến trên khoảng nào sau đây A. (-1;0). B. (-6;-3). C. (3;6). D. (6;+∞).
Đọc tiếp
Cho hàm số f(x) có đồ thị của hàm số y=f’(x) như hình vẽ:
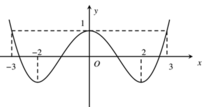
Hàm số y = f ( 2 x - 1 ) + x 3 3 + x 2 - 2 x nghịch biến trên khoảng nào sau đây
A. (-1;0).
B. (-6;-3).
C. (3;6).
D. (6;+∞).
Cho hàm số f(x), đồ thị hàm số yf (x) là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x) -f(2x-1) +2x trên đoạn [0;2] bằng
Đọc tiếp
Cho hàm số f(x), đồ thị hàm số y=f '(x) là đường cong trong hình bên. Giá trị lớn nhất của hàm số g(x) = -f(2x-1) +2x trên đoạn [0;2] bằng
Lời giải:
$g(x)=2x-f(2x-1)$
$g'(x)=2-2f'(2x-1)=2[1-f'(2x-1)]=0$
$\Leftrightarrow f'(2x-1)=1$
$\Leftrightarrow x=0;x=1; x=\frac{3}{2}$
Lập bảng biến thiên với các mốc $0; 1;\frac{3}{2};2$ ta thấy $g(x)$ đạt max tại $x=\frac{3}{2}$, tức là $g(x)_{\max}=-f(2)+3$
Đúng 1
Bình luận (1)
Cho F(x) là nguyên hàm của hàm số
f
x
2
x
+
1
8
x
+
1
10
thỏa mãn F(0)1. Tìm hàm số F(x). A.
F
x
1...
Đọc tiếp
Cho F(x) là nguyên hàm của hàm số f x = 2 x + 1 8 x + 1 10 thỏa mãn F(0)=1. Tìm hàm số F(x).
A. F x = 1 8 2 x + 1 x + 1 8 + 7 8
B. F x = 1 9 ln 2 x + 1 x + 1 + 8 9
C. F x = 1 9 2 x + 1 x + 1 9 + 8 9
D. F x = − 1 9 x + 1 2 x + 1 9 + 10 9
Cho hàm số y f(x) có đạo hàm liên tục trên R, thỏa mãn
2
f
(
2
x
)
+
f
(
1
-
2
x
)
12
x
3
. Tìm phương trình tiếp tuyến của đồ thị hàm số y f(x) tại điểm có hoành độ x 1 A. B. C. D.
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên R, thỏa mãn 2 f ( 2 x ) + f ( 1 - 2 x ) = 12 x 3 . Tìm phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y=f(x) có đạo hàm trên R và thỏa mãn f(1+3x)=2x-f(1-2x) với mọi \(x\in R\) . Lập phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=1 .
Lời giải:
Từ $f(1+3x)=2x-f(1-2x)$ thay $x=0$ suy ra $f(1)=1$
$f(1+3x)=2x-f(1-2x)$
$\Rightarrow f'(1+3x)=(2x)'-f'(1-2x)$
$\Leftrightarrow 3f'(1+3x)=2+2f'(1-2x)$. Thay $x=0$ suy ra $f'(1)=2$
PTTT của $f(x)$ tại điểm $x=1$ là:
$y=f'(1)(x-1)+f(1)=2(x-1)+1=2x-1$
Đúng 1
Bình luận (2)
Cho hàm số f(x) có đạo hàm
f
(
x
)
x
(
x
+
1
)
(
x
+
2
)
3
,
∀
x
∈
R
. Số điểm cực trị của hàm số
y
f
(
x
2
-
2
x
)
là A. 3. B. 2. C. 5. D. 4.
Đọc tiếp
Cho hàm số f(x) có đạo hàm f ' ( x ) = x ( x + 1 ) ( x + 2 ) 3 , ∀ x ∈ R . Số điểm cực trị của hàm số y = f ( x 2 - 2 x ) là
A. 3.
B. 2.
C. 5.
D. 4.
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x - 1 ) 2 ( x - 3 ) 3 ( 2 x + 3 ) , ∀ x ∈ ℝ . Số cực trị của hàm số đã cho là
A. 1
B. 2
C. 0
D. 3