Cho AB // EG và một điểm C bất kì như hình vẽ và A = 40o ; E = 50o. Chứng minh rằng AC vuông góc với CE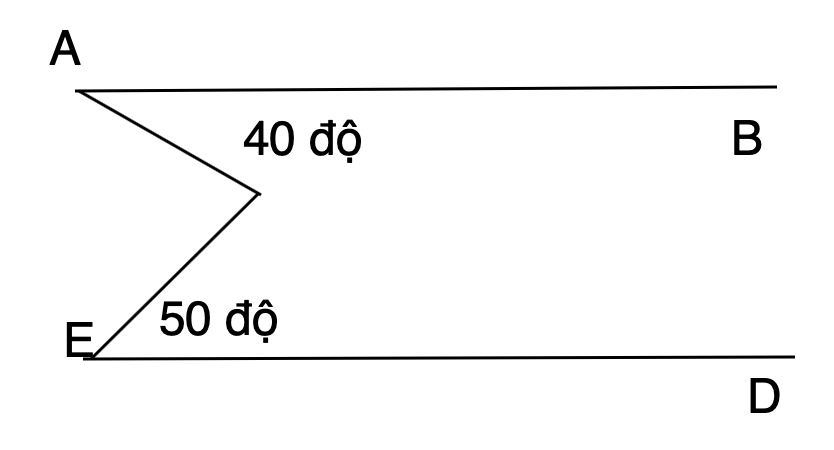

Những câu hỏi liên quan
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?

a)

b) Đoạn thẳng AB cắt đường thẳng xy
Đúng 0
Bình luận (0)
Vẽ hình theo cách diễn đạt bằng lời sau:
a) Cho góc xOy bằng 65 degrees . M là một điểm bất kì nằm trong góc xOy. Vẽ MA vuông góc Ox (A thuộc (x) AB vuông góc với Oy ( B thuộc (y) Vẽ đường thẳng d qua M và song song với Oy.
b) Cho ba điểm A, B, C bất kì. Hãy vẽ các đường trung trực của các đoạn thẳng AB, BC, CA.
cứu gấp ạ
Bài 4: Cho đoạn thẳng AB. Lấy điểm C bất kì nằm giữa A và B. Vẽ về cùng một phía của AB các hình vuông ACDE và BCPQ.
a) CMR: AP = BD
b) M và N lần lượt là trung điểm AP và BD. CMR: CM = CN
c) CMR: CM vuông góc CN.
d) CMR: AP vuông góc BD.
Hộp giấy có các mặt là hình vuông ở Hình 1a được vẽ lại với các đỉnh là \(A,B,C,D,A',B',C',D'\) như Hình 1b. Gọi tên cặp mặt phẳng:
a) Có ba điểm chung không thẳng hàng.
b) Là hai mặt phẳng phân biệt và có một điểm chung.
c) Không có bất kì điểm chung nào.
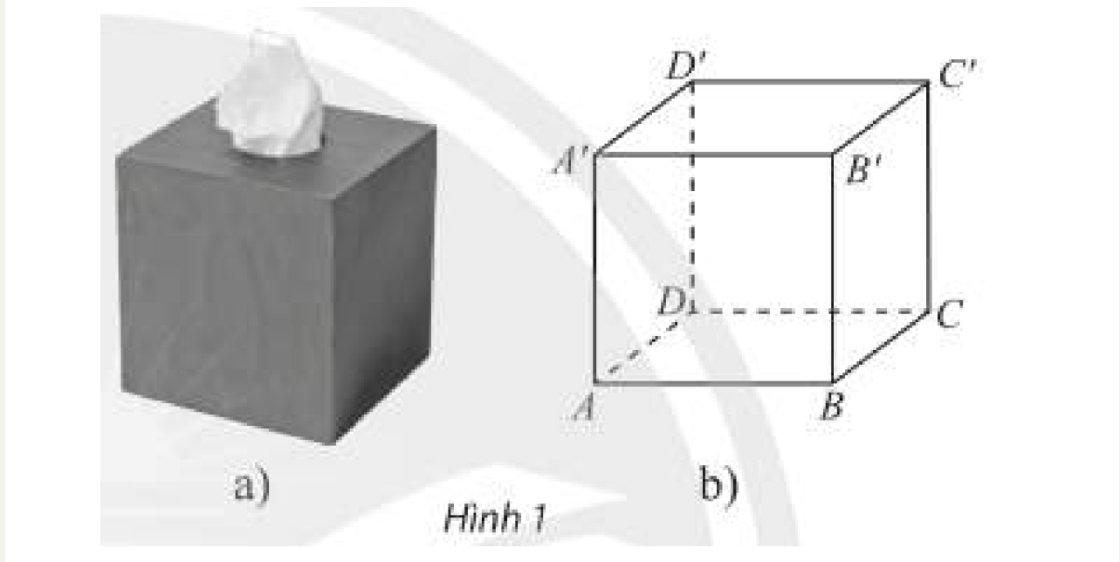
a: (ABC) và (ABD); (A'B'C') và (A'B'D'); (AA'B) và (AA'B'),...
b: Không có hai mp phân biệt nào có 1 điểm chung
c: (ABCD) và (A'B'C'D')
(ABB'A') và (CDD'C')
Đúng 0
Bình luận (0)
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
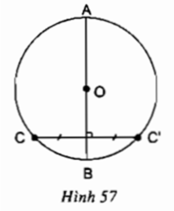
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
Cho đường tròn (O), AB là một đường kính bất kì và C là một điểm thuộc đường tròn. Vẽ C’ đối xứng với điểm C qua AB (h.57). Chứng minh rằng điểm C’ cũng thuộc đường tròn (O).
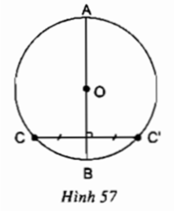
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)
Đúng 0
Bình luận (0)
cho đoạn thẳng AB và một điểm c bất kì nằm giữa A và B
Bài 5. Cho hình chữ nhật ABCD. Nối C với một điểm E bất kì trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại H và K. Chứng minh:
a) Tứ giác AHFK là hình chữ nhật
b) AF // BD;
c) Ba điểm E, H, K thẳng hàng.
a: Xét tứ giác AHFK có
góc AHF=góc AKF=góc KAH=90 độ
=>AHFK là hình chữ nhật
b: Gọi O là giao của AC và BD, I là giao của AF và HK
AHFK là hình chữ nhật
=>I là trung điểm chung của AF và HK
ABCD là hình chữ nhật
=>O là trung điểm chung của AC và BD
Xét ΔAFC có I,O lần lượt là trung điểm của AF,AC
=>IO là đường trung bình
=>IO//FC và IO=FC/2
=>IO//FE và IO=FE
Xét tứ giác IFEO có
IO//FE
IO=FE
=>IFEO là hình bình hành
=>IF//OE
=>AF//BD
Đúng 1
Bình luận (0)
cho hình chữ nhật abcd có e va glan lượt là điểm chính giữa của ad và bc .m; n là điểm bất kì lần lượt trên ab và cd . mn cat eg tại i
so sanh
Sabge va S abcd
mi va in














