tôi ko bt, lêu lêu

Áp dụng định lí Pytago ta có

\(a,BC^2=AB^2+BC^2=12^2+16^2\\ =\sqrt{400}=20\\ b,BD^2=BC^2+CD^2\\ 5^2=3^2+CD^2\\ CD^2=5^2-3^2=\sqrt{16}=4\)

\(a,AB=\cos B\cdot BC=6\left(cm\right)\\ AC=\sqrt{BC^2-AB^2}=6\sqrt{3}\left(cm\right)\\ b,\text{Áp dụng HTL: }AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{3}\left(cm\right)\)

ΔABC vuông tại A

=>AB^2+AC^2=BC^2

=>AB^2=15^2-12^2=81

=>AB=9cm

Xét ΔABC vuông tại A có sin C=AB/BC=9/15=3/5

nên góc C=37 độ

=>góc B=53 độ

Xét tam giác ABC vuông tại A áp dụng Py-ta-go ta có:

\(AB^2+AC^2=BC^2\)

\(\Rightarrow AB=\sqrt{BC^2-AC^2}\)

\(\Leftrightarrow AB=\sqrt{15^2-12^2}=9\left(cm\right)\)

Xét tam giác ABC vuông tại A ta có: 

\(sinC=\dfrac{AB}{BC}=\dfrac{9}{15}=\dfrac{3}{5}\)

\(\Rightarrow\widehat{C}\approx37^o\)

Mà: \(\widehat{C}+\widehat{B}=90^o\)

\(\Leftrightarrow\widehat{B}=90^o-37^o=53^o\)

tự làm đi cu, dễ vl ra

a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A

\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)

\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)

* Áp dụng hệ thức : 

\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)

\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)

\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm 

\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm

\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)

Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm²

b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)

Lại có : \(BC=BD+DC=15+20=35\)cm 

Áp dụng định lí Pytago cho tam giác ABC vuông tại A

\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)

\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm 

\(\Rightarrow AB=\frac{3}{4}.28=21\)cm 

* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)

\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm 

* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm 

\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm

Áp dụng định lí Pytago cho tam giác AHD vuông tại H 

\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm 

2 tam giác chung ABCD là sao bn?

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=5^2+12^2=169\)

=>\(BC=\sqrt{169}=13\left(cm\right)\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{5}{13}\)

nên \(\widehat{B}\simeq23^0\)

Ta có: ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{C}\simeq90^0-23^0=67^0\)

b: Ta có: ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{C}=90^0-40^0=50^0\)

Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)

=>\(BC=\dfrac{AC}{sinB}=\dfrac{5}{sin40}\simeq7,78\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AB^2=BC^2-AC^2\)

=>\(AB\simeq\sqrt{7,78^2-5^2}\simeq5,96\left(cm\right)\)

Hình vẽ:

Giải

a. Xét ΔHBA và ΔABC có:

\(\widehat{B}\)  chung

\(\widehat{BHA}=\widehat{BAC}=90^0\)

⇒ΔHBA ∼ ΔABC (g.g)

b. Xét ΔABC vuông tại A có:

\(BC^2=AB^2+AC^2\)(định lí py-ta-go)

         \(=5^2+12^2\)

         \(=169\)

\(\rightarrow BC=\sqrt{169}=13\left(cm\right)\)

Vì ΔABC ∼ ΔHBA (cmt)

\(\rightarrow\dfrac{AB}{BH}=\dfrac{AC}{AH}=\dfrac{BC}{AB}hay\dfrac{5}{BH}=\dfrac{12}{AH}=\dfrac{13}{5}\)

⇒\(BH=\dfrac{5.5}{13}=\dfrac{25}{13}\left(cm\right)\)

⇒\(AH=\dfrac{12.5}{13}=\dfrac{60}{13}\left(cm\right)\)

Xét tam giác ABC vuông tại A có:

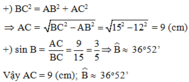
Đáp án cần chọn là: B