Câu 6:Cho tam giác vuông ABC (vuông ở A), biết AB = 6cm; AC = 8cm; BC = 10cm. Tính độ dài chiều cao hạ từ đỉnh A xuống cạnh đáy BC.
Trả lời: Độ dài chiều cao hạ từ đỉnh A xuống cạnh đáy BC là cm
(Nhập kết quả dưới dạng số thập phân thu gọn)

Những câu hỏi liên quan
Cho tam giác ABC vuông góc A biết AB=6cm,BC=10cm, biết AB=6cm a)tính độ dài AC b) đường phân giác của góc ABC cắt cạnh AC ở E . Kẻ EH vuông góc BC (H thuộc BC). chứng minh rằng tam giác ABE= tam giác HBE c)gọi K là giao điểm của đường thẳng AB,HE. Chứng minh rằng tam giác EAC cân d) chứng minh đường thẳng BE là đường trung trực của AC
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=10^2-6^2=64\)
hay AC=8(cm)
Vậy: AC=8cm
b) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (0)
1. Cho tam giác ABC vuông tại A, biết AH 16, BH 9. Tính AB.2. Cho tam giác ABC vuông tại A, AB 6cm, AC 8cm. Tính độ dài HB.3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12, BC 15. Tính HC.4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 6, HC 9. Tính độ dài AC.5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12cm, BC 16cm. Tính AH6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 8cm, HC 12 cm. Tính AC.
Đọc tiếp
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (3)
ai biết giải giúp minh với:Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minha,tứ giác HECD nội tiếpb,Tia DA là tia phân giác góc EDK Cây 2:cho tam giác ABC vuông tai A,biết ab6cm,ac8cmA.tính bcB,kẻ đường cao AH,tính Ah Câu 3:Cho tam giác abc vuông tại A,BIẾT AC4cm,Bc5cm.A,Tính cạnh ABB,kẻ đường cao AH,TÍNH AHCâu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB12CM,AC5CM.tính BH,CHCâu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC18cm,B...
Đọc tiếp
ai biết giải giúp minh với:
Câu 1:Cho tam giác ABC có 3 góc nhọn,các đường cao AD,BE,CK cắt nhau tại H.chứng minh
a,tứ giác HECD nội tiếp
b,Tia DA là tia phân giác góc EDK
Cây 2:cho tam giác ABC vuông tai A,biết ab=6cm,ac=8cm
A.tính bc
B,kẻ đường cao AH,tính Ah
Câu 3:Cho tam giác abc vuông tại A,BIẾT AC=4cm,Bc=5cm.
A,Tính cạnh AB
B,kẻ đường cao AH,TÍNH AH
Câu 4:Cho tam giác vuông ABC,vuông tại A(H thuộc BC).bIẾT AB=12CM,AC=5CM.tính BH,CH
Câu 5:cho tam giác ABC vuông tại A,đường cao AH(H THUỘC BC).biết BC=18cm,BH=6cm.Tính độ dài các cạnh AB,AC
Cau 6:Cho tam giác ABC,vuông tại A,biết AB=4cm,đường cao AH=2CM,tính các góc và các cạnh còn lại cua tam giac.?
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
Đúng 1
Bình luận (0)
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
Đúng 0
Bình luận (0)
cho tam giác vuông ABC (vuông ở A), biết AB= 6cm, AC = 8cm, BC=10cm. Tính độ dài chiều cao hạ từ đỉnh A xuống cạnh đáy BC. Ai làm được câu này đầu tiên tôi tích cho
Đáp số: 4,8 cm.
Đúng 100% luôn!
Ai tk cho mình mình tk lại.
Đúng 0
Bình luận (0)
Giải
DT hình tam giác ABC là :
6 x 8 : 2 = 24 ( cm2 )
Độ dài chiều cao hạ từ đỉnh A xuống cạnh đáy BC là :
24 x 2 : 10 = 4,8 ( cm )
Đ/S : 4,8 cm
Đúng 0
Bình luận (0)
Hình cậu tự vẽ nha ?
Giải
Diện tích tam giác ABC LÀ ; 8x6;2 = 24 (cm2)
Độ dài đáy từ đỉnh A xuống đáy BC là :
24 x 2 : 10 = 4,8 ( cm )
Đ/S : .........
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
6. Cho tam giác ABC vuông ở A đường cao AH, biết AB = 6cm, AC =8cm. a/ Tính AH; b/ Tính góc HAC; c/ Từ H kẻ HE AB, HF AC. Tính EF
a)Áp dụng đl pytago ta có:
`BC^2=AB^2+AC^2=36+64=100`
`<=>BC=10cm`
Áp dụng HTL vào tam giác vuông ABC ta có:
`AH.BC=AB.AC`
`<=>10AH=48`
`<=>AH=4,8cm`
b)Xét tam giác vuông HAC ta có:
`cos hat{HAC}=(AH)/(AC)=3/5`
`=>hat{HAC}=53^o`
Đúng 1
Bình luận (0)
- Áp dụng định lý pitago vào tam giác ABC vuông tại A .
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
- Áp dụng hệ thức lượng vào tam giác vuông ABC đường cao AH .
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b, - Áp dụng tỉ số lượng giác vào tam giác HAC
Có : \(\cos A2=\dfrac{AH}{AC}=\dfrac{3}{5}\)
\(\Rightarrow\widehat{A2}\approx53^o\)15,
c, - Đề không rõ bạn ơi ;-;
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A có AB = 6cm ; BC = 10cm trên cạnh BC lấy điểm D sao cho BD = 6cm vẽ đường vuông góc với BC cắt cạnh AC tại M câu a tính AC câu b tính chu vi tam giác ABC câu c chứng minh BM là đường phân giác của tam giác ABC
Cho tam giác ABC vuông tại C, kẻ CH \(\perp\)AB, HN vuông góc với BC, HM vuông góc với AC.
a) c/m: CM.CA=CN.CB.
b) Biết CH=6cm, AB=13cm. tính diện tích tứ giác CMHN.
Giúp câu b với a.
a: Xét ΔCHA vuông tại H có HM là đường cao
nên \(CM\cdot CA=CH^2\left(1\right)\)
Xét ΔCHB vuông tại H có HN là đường cao
nên \(CN\cdot CB=CH^2\left(2\right)\)
Từ (1) và (2) suy ra \(CM\cdot CA=CN\cdot CB\)
Đúng 0
Bình luận (0)
Phần tự luận
Nội dung câu hỏi 1
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
a) Tính BC, ∠B, ∠C
a) Xét tam giác ABC vuông tại A có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
⇒ BC = 10 (cm)

∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0
Đúng 0
Bình luận (0)
Câu 6 Cho tam giác ABC vuông tại A, M là trung điểm của BC. Kẻ MD // AB, ME // AC (D AC, E AB). a) Chứng minh tứ giác ADME là hình chữ nhật.b) Cho AM 10cm, AD 6cm. Tính MD?c) Tam giác ABC cần thêm điều kiện gì để tứ giác ADME là hình vuông?
Đọc tiếp
Câu 6 Cho tam giác ABC vuông tại A, M là trung điểm của BC. Kẻ MD // AB, ME // AC (D ![]() AC, E
AC, E ![]() AB).
AB).
a) Chứng minh tứ giác ADME là hình chữ nhật.
b) Cho AM = 10cm, AD = 6cm. Tính MD?
c) Tam giác ABC cần thêm điều kiện gì để tứ giác ADME là hình vuông?
Hình tự vẽ nhe fen :
a)
Tú giác ADME có:
MD // AB (gt)
ME // AC (gt)
góc A = 90 độ (gt)
=> tứ giác ADME là hình chữ nhật
b)
Vì Tứ giác ADME là hình chữ nhật => Góc MDA = Góc A = Góc MEA = góc EMD = 90 độ ( tính chất hình chữ nhật )
Tam giác ADM có:
Góc MDA = 90 độ
=> Tam giác ADM vuông góc tại D
Áp dụng định lí pitago vào tam giác ADM ta có:
\(AM^2=AD^2+MD^2\Rightarrow MD=8\left(cm\right)\)
c)
Giả sử Tam giác ABC vuông cân:
=> theo bài ra ta có: ME//AC, MD//AB, góc A vuông => Tứ giác ADME là hình chữ nhật (1)
Xét Tam giác ABC có:
ME//AC (gt)
M là trung điểm của BC (gt)
=> ME là đường trung bình của tam giác ABC
=> ME=1/2 AC (tc đường trung bình)
Ta lại có:
tam giác ABC có:
MD//AB (gt)
M là trung điểm của BC (gt)
=> MD là đường trung bình của tam giác ABC
=> MD=1/2AB
Mà Tam giác ABC vuông cân => AC=AB (tính chất tam giác cân)
=> MD=ME=1/2AB=1/2AC (2)
Từ (1) và (2) => Tứ giác ADME là Hình vuông
=> Để tứ giác ADME là hình vuông thì tam giác ABC phải là Tam giác Vuông cân tại A
Đúng 1
Bình luận (1)
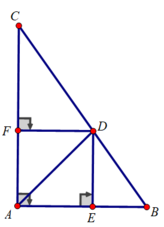
Câu 6. Cho tam giác ABC vuông tại A, đường phân giác BE, kẻ EH vuông góc với BC
tại H, gọi K là giao điểm của hai đường thẳng BA và HE.
a) Chứng minh AE = HE, AB = BH.
b) Chứng minh tam giác BCK là tam giác cân.
c) Tính độ dài BK, AC biết AB = 6cm, BC = 10cm.
Cm : Xét t/giác ABE và t/giác AHE
có góc A1 = góc H1 = 900 (gt)
BE : chung
góc B1 = góc B2 (gt)
=> t/giác ABE = t/giác AHE (ch - gn)
=> AE = HE; AB = HB (các cặp cạnh tương ứng)
b) Ta có: góc A1 + góc A2 = 1800 (kề bù)
=> góc A2 = 1800 - góc A1 = 1800 - 900 = 900
=> góc A1 = góc H2 = 900
Xét t/giác AEK và t/giác HEC
có góc A2 = góc H2 = 900 (cmt)
AE = HE (cmt)
góc E1 = góc E2 (Đối đỉnh)
=> t/giác AEK = t/giác HEC (g.c.g)
=> AK = HC (hai cạnh tương ứng)
Mà AB + AK = BK
BH + HC = BC
Và AB = HB (cmt)
=> BK = BC
=> t/giác BKC là t/giác cân tại B
c) Áp dụng định lý Py - ta - go vào rồi lm
#zinc































