Cho tam giác ABC, biết AB = 21 ; AC = 28 ; BC = 35
a) Chứng minh rằng tam giác ABC vuông
b) Tính sinB, sinC, góc B, góc C và đường cao AH vủa tam giác ABC
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3 : 4 và AB + AC = 21. Tính các canh của tam giác ABC
A. AB = 9; AC = 10; BC = 15
B. AB = 9; AC = 12; BC = 15
C. AB = 8; AC = 10; BC = 15
D. AB = 8; AC = 12; BC = 15
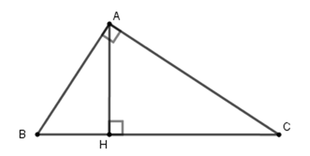
Theo giả thiết AB : AC = 3 : 4
Suy ra A B 3 = A C 4 = A B + A C 3 + 4 = 3 . Do đó AB = 3.3 = 9 (cm); AC = 3.4 = 12 (cm)
Tam giác ABC vuông tại A, theo định lý Pytago ta có:
B C 2 = A B 2 + A C 2 = 9 2 + 12 2 = 225 , suy ra BC = 15cm
Đáp án cần chọn là: B
Cho tam giác ABC có góc A=90độ. biết AB-AC=21 . tính các cạnh của tam giác ABC
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC
\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)
\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)
\(BC=\sqrt{AB^2+AC^2}=841\)
Chu vị: \(609+580+841=2030\)
Ta có: \(\dfrac{AB}{AC}=\dfrac{20}{21}\)
nên \(AB=\dfrac{20}{21}\cdot AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{400}{441}AC^2}+\dfrac{\dfrac{400}{441}}{\dfrac{400}{441}AC^2}=\dfrac{1}{176400}\)
\(\Leftrightarrow\dfrac{400}{441}AC^2=336400\)
\(\Leftrightarrow AC^2=370881\)
hay AC=609(cm)
\(\Leftrightarrow AB=\dfrac{20}{21}\cdot AC=\dfrac{20}{21}\cdot609=580\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=580^2+609^2=371461\)
hay BC=841(cm)
Chu vi tam giác ABC là:
AB+AC+BC=580+609+841=2030(cm)
Cho tam giác ABC vg tại A, đg cao AH. Biết AB/AC= 20/21 và AH=420. Tính chu vi tam giác ABC
Tam giac ABC đồng dạng tam giác HAC (cùng vuông và có chung góc C)
AB/AC = AH/HC = 20/21
HC = 21AH/20 = 441
==> AC = căn(AH^2 + HC^2) =căn(420^2 + 441^2) = 609
AB/AC = 20/21
AB = 20/21*609 = 580
BC = căn(AB^2 + AC^2) = căn(580^2 + 609^2) = 841
Chu vi tam giác ABC = tổng 3 cạnh
C = AB + AC + BC = 580 + 609 + 841 = 2030
Tính các cạnh của tam giác ABC biết AB - AC = 21 và tam giác ABC vuông tại A
Cho tam giác abc vuông tại A, đường cao AH, biết AB=21 cm, AC=28cm
a) Tính Ah
b) KẺ HD vuông góc AB, HE vuông góc AC. Tính diện tích tam giác AED
a:
BC=35cm
\(AH=\dfrac{AB\cdot AC}{BC}=16.8\left(cm\right)\)
b: \(AE=\dfrac{AH^2}{AC}=\dfrac{16.8^2}{28}=10.08\left(cm\right)\)
\(AD=\dfrac{AH^2}{AB}=\dfrac{16.8^2}{21}=13.44\left(cm\right)\)
Do đó: \(S_{AED}=\dfrac{AD\cdot AE}{2}=\dfrac{13.44\cdot10.08}{2}=67.7376\left(cm^2\right)\)
Cho tam giác ABC vuông tại A biết AB = 21 cm, C ^ = 40 0 . Tính độ dài đường phân giác BD của A B C ^ , với D nằm trên cạnh AC
A B D ^ = 25 0 . Áp dụng tỉ số lượng giác trong tam giác vuông ABD ta có: BD = 21 cos 25 0 ≈ 21 , 19 c m
cho tam giác abc , ad là phân giác của góc bac, biết ab=9, ac=21. tính tỉ số của bd và dc
Cho tam giác ABC. Trên BC lấy điểm M sao cho BM = MC. MH là đường cao của tam giác ABM, MQ là đường cao của tam giác ACM. Cho MH = 3 cm, MQ = 6 cm
a ) So sánh AB và AC
b ) Tính diện tích ABC biết AB + AC = 21 cm
Bài làm
Ta có hình vẽ :
a ) Tam giác AMB và AMC có đáy MC = MB và có chung chiều cao hạ từ A xuống MC nên SAMC = SAMB
Mà diện tích của tam giác AMC là : ( MQ + AC ) : 2 = 6 x AC : 2 = 3 x AC
Mà diện tích của tam giác AMB là : ( MC x AB ) : 2 = 3 x AB : 2 = 1,5 x AB
Vì SAMC = SAMB nên 3 x AC = 1,5 x AB = > 2 x AC = AB
b ) Đáy BC dài là : 21 : ( 2 + 1 ) x 2 = 14 ( cm )
Diện tích tam giác AMB là : ( 14 x 3 ) : 2 x 2 = 42 ( cm2 )
Cho tam giác ABC vuông tại A biết AC = 21 cm và AB = 18 cm. Tìm khẳng định sai ?
A. C ^ = 41 °
B. B ^ = 49 °
C. B ^ = 50 °
D. B C = 3 85