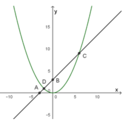
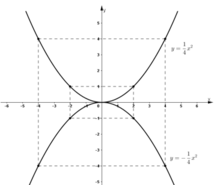
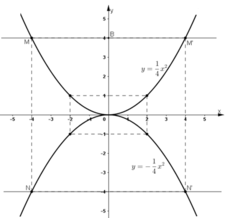
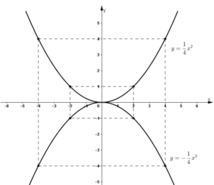
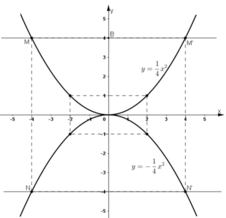
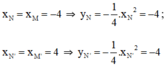Vẽ đồ thị của hàm số y=14x2y=14x2 và y=−14x2y=−14x2 trên cùng một hệ trục tọa độ
a) Qua điểm B(0; 4) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số y=14x2y=14x2 tại hai điểm M và M’. Tìm hoành độ của M và M’.
b) Tìm trên đồ thị của hàm số y=−14x2y=−14x2 điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:
- Ước lượng trên hình vẽ:
- Tính toán theo công thức.






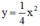
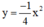
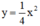
 tại N và N’.
tại N và N’.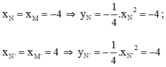
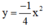 điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ điểm N và N’ bằng hai cách:
điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ điểm N và N’ bằng hai cách: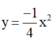 tại N và N’.
tại N và N’.