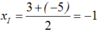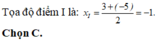Tọa độ a = (-3 ; 2) b = (4;3) Tìm tọa độ M sao cho tam giác ABC vuông tại M

Những câu hỏi liên quan
Cho hình vuông ABCD có A có tọa độ -2 -3, B có tọa độ -2 3, C có tọa độ 4 3. Xác định D
em gửi bài qua fb thầy chữa cho, tìm fb của thầy bằng sđt nhé: 0975705122
Đúng 0
Bình luận (0)
cíu mình với :(
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh A B C (1; 2) (3; -1) ; (4; 5 ). a. Tìm tọa độ các vectơ AB AC ; b. Tìm tọa độ trung điểm I của đoạn BC
Trên trục tọa độ
O
;
i
→
cho 2 điểm A ; B có tọa độ lần lượt 3 và – 5.Tọa độ trung điểm I của AB là : A. 2 B. 4 C. -1 D. -2
Đọc tiếp
Trên trục tọa độ O ; i → cho 2 điểm A ; B có tọa độ lần lượt 3 và – 5.Tọa độ trung điểm I của AB là :
A. 2
B. 4
C. -1
D. -2
Trên trục tọa độ
(
O
;
i
→
)
cho 2 điểm A ; B có tọa độ lần lượt 3 và – 5. Tọa độ trung điểm I của AB là : A. 2 B. 4 C. -1 D.-2
Đọc tiếp
Trên trục tọa độ ( O ; i → ) cho 2 điểm A ; B có tọa độ lần lượt 3 và – 5. Tọa độ trung điểm I của AB là :
A. 2
B. 4
C. -1
D.-2
Cho tam giác ABC có tọa độ 3 đinh là A(4; 1), B(3; 2), C(1;6).Viết phương trình: f) đường thẳng đi qua A và tạo với hai trục tọa độ một tam giác cân đỉnh là gốc tọa độ
Đối xứng của A qua trục tung là A'(4; -1) và đối xứng của A qua trục hoành là A"(-4; 1).
Vậy đỉnh thứ hai của tam giác cân là I(-4; -1).
Ta có thể tính được hệ số góc của đường thẳng AI bằng công thức:
\(m=\dfrac{y_A-y_I}{x_A-x_I}=\dfrac{1-\left(-1\right)}{4-\left(-4\right)}=\dfrac{1}{4}\)
Vậy phương trình đường thẳng AI là:
\(y-y_A=m\left(x-x_A\right)\)
\(y-1=\dfrac{1}{4}\left(x-4\right)\)
\(4y-4=x-4\)
\(x-4y=0\)
Vậy phương trình đường thẳng cần tìm là \(x-4y=0\)
Đúng 1
Bình luận (0)
Đường thẳng đi qua A và tạo với hai trục tọa độ một tam giác cân đỉnh là gốc tọa độ sẽ qua điểm trung điểm của đoạn thẳng BC, ký hiệu là M.
Có:
Tọa độ x của trung điểm M = \(\dfrac{x_B+x_C}{2}=\dfrac{3+1}{2}=2\)
Tọa độ y của trung điểm M = \(\dfrac{y_B+y_C}{2}=\dfrac{2+6}{2}=4\)
Vậy tọa độ của điểm M là (2, 4).
Phương trình đường thẳng đi qua A và M là:
\(y-1=\dfrac{4-1}{2-4}.\left(x-4\right)\Rightarrow y=-1,5x+7\)y
Vậy phương trình đường thẳng cần tìm là \(y=-1,5x+7.\)
(Cái câu kia mình làm cho bài khác tính cop màn hình mà bấm gửi nhầm ở đây, bài giải này mới đúng nhé!)
Đúng 1
Bình luận (0)
Cho 3 điểm A(3;-5) B(-2;-2) C(4;1)
a) Tìm tọa độ vecto BC, vecto AC, vecto BA
b) Chứng minh rằng ba điểm A,B,C không thẳng hàng
c) Tìm tọa đọ trung điểm I của AC; J của AB
d) Tìm tọa độ trọng tâm G của tam giác ABC
e) Tìm tọa độ điểm H sao cho A là trọng tâm tam giác HBC
g) Tìm tọa độ điểm D sao cho ABCD là hình bình hành
Cho 3 điểm A(-3;2);B(0;4);C(1;-1)
a,3 điểm A,B,C có thẳng hàng không
b,Tính chu vi Tam giác ABC
c,Tìm tọa độ trung điểm AB,BC,CA
đ,Tìm tọa độ trọng tâm Tam giác ABC
e,Tìm tọa độ Đ sao cho ABCD là hình bình hành
f,Tìm tọa độ E sao cho ABCD là hình bình hành
a) Ta thấy \(\overrightarrow{AB}\left(3;2\right)\) và \(\overrightarrow{AC}\left(4;-3\right)\). Vì \(\dfrac{3}{4}\ne\dfrac{2}{-3}\) nên A, B, C không thẳng hàng.
b) Ta có \(\overrightarrow{BC}\left(1;-5\right)\)
Do vậy \(AB=\left|\overrightarrow{AB}\right|=\sqrt{3^2+2^2}=\sqrt{13}\)
\(AC=\left|\overrightarrow{AC}\right|=\sqrt{4^2+\left(-3\right)^2}=5\)
\(BC=\left|\overrightarrow{BC}\right|=\sqrt{1^2+\left(-5\right)^2}=\sqrt{26}\)
\(\Rightarrow C_{ABC}=AB+AC+BC=5+\sqrt{13}+\sqrt{26}\)
c) Gọi M, N, P lần lượt là trung điểm BC, CA, AB.
\(\Rightarrow P=\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)=\left(-\dfrac{3}{2};3\right)\)
\(N=\left(\dfrac{x_A+x_C}{2};\dfrac{y_A+y_C}{2}\right)=\left(-1;\dfrac{1}{2}\right)\)
\(M=\left(\dfrac{x_B+x_C}{2};\dfrac{y_B+y_C}{2}\right)=\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)
d) Gọi G là trọng tâm tam giác ABC thì \(G=\left(\dfrac{x_A+x_B+x_C}{3};\dfrac{y_A+y_B+y_C}{3}\right)=\left(-\dfrac{2}{3};\dfrac{5}{3}\right)\)
e) Gọi \(D\left(x_D;y_D\right)\) là điểm thỏa mãn ycbt.
Để ABCD là hình bình hành thì \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left(3;2\right)=\left(1-x_D;-1-y_D\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}3=1-x_D\\2=-1-y_D\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=-2\\y_D=-3\end{matrix}\right.\)
\(\Rightarrow D\left(-2;-3\right)\)
f) Bạn xem lại đề nhé.
Đúng 0
Bình luận (0)
1/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= -2x + 3 b) (P) : y = x² c) Tìm tọa độ giao điểm của hai đồ thị 2/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= -x + 3 b) (P) : y = 2x² c) Tìm tọa độ giao điểm của hai đồ thị 3/ Vẽ (D) và (P) trên cùng một hệ trục tọa độ a) (D) : y= x - 3 b) (P) : y = -3x² c) Tìm tọa độ giao điểm của hai đồ thị
1:
a: 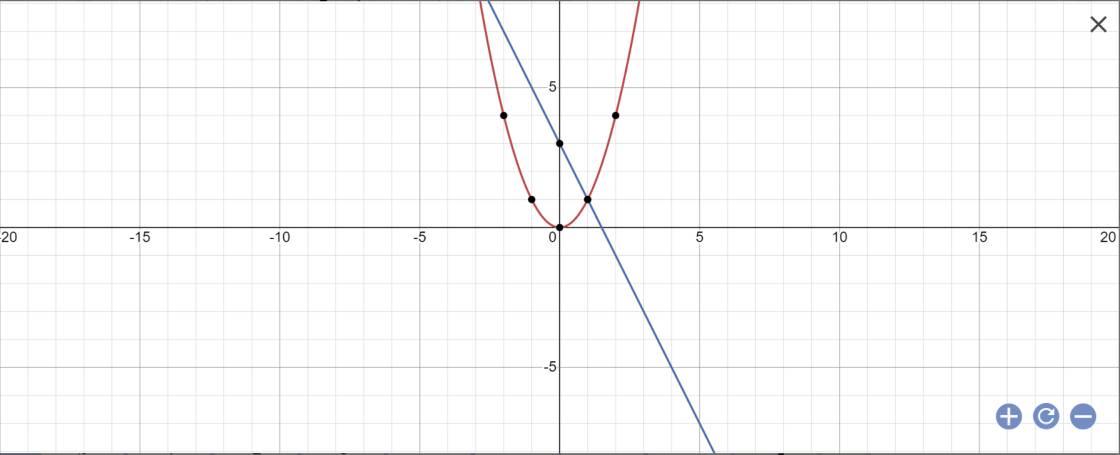
b: PTHĐGĐ là:
x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
=>y=9 hoặc y=1
Đúng 0
Bình luận (0)
Cho tam giác ABC có tọa độ 3 đinh là A(4; 1), B(3; 2), C(1; 6).Viết phương trình: f) đường thẳng đi qua A và tạo với hai trục tọa độ một tam giác cân đỉnh là gốc tọa độ.
Trong hệ tọa độ Oxy ; cho tam giác ABC có A(-2 ; 2) : B(3 ; 5) và trọng tâm là gốc tọa độ O(0 ; 0). Tìm tọa độ đỉnh C? A. C(-1 ; - 7) B. C( 2 ; -2) C. C(-3 ; -3) D. (1 ; 7)
Đọc tiếp
Trong hệ tọa độ Oxy ; cho tam giác ABC có A(-2 ; 2) : B(3 ; 5) và trọng tâm là gốc tọa độ O(0 ; 0). Tìm tọa độ đỉnh C?
A. C(-1 ; - 7)
B. C( 2 ; -2)
C. C(-3 ; -3)
D. (1 ; 7)