Có bao nhiêu giá trị nguyên của m ∈ ( - 10 ; 10 ) để hàm số y = m 2 x 4 - 2 ( 4 m - 1 ) x 2 + 1 đồng biến trên khoảng ( 1 ; + ∞ )
A. 15
B. 7
C. 16
D. 6
Có bao nhiêu giá trị nguyên của tham số m (m < 10) để phương trình 2 x - 1 = log 4 x + 2 m + m có nghiệm ?
A.9
B.10
C.5
D.4
Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình m + m + e x = e x có nghiệm thực?
A. 9
B. 10
C. 11
D. Vô số
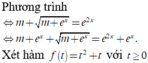 và đi đến kết quả
và đi đến kết quả
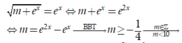 có 10 giá trị thỏa mãn. Chọn B.
có 10 giá trị thỏa mãn. Chọn B.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10; 10] để phương trình m x 2 - m x + 1 = 0 có nghiệm.
A. 17
B. 18
C. 20
D. 21
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
Câu 38/Đề 7: Có bao nhiêu giá trị nguyên thuộc [-10;10] của m để giá trị lớn nhất của hàm số y=-x^4 +4x- m trên đoạn [-1;3] nhỏ hơn 10
Để tìm số giá trị nguyên của m trong khoảng [-10;10] sao cho giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3] nhỏ hơn 10, chúng ta cần thực hiện các bước sau:
1. Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
2. Kiểm tra xem giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
3. Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Bước 1: Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
Để tìm giá trị lớn nhất, chúng ta có thể lấy đạo hàm của hàm số và giải phương trình đạo hàm bằng 0.
y' = -4x^3 + 4
Để tìm giá trị của x khi đạo hàm bằng 0, giải phương trình:
-4x^3 + 4 = 0
X^3 - 1 = 0
( x - 1)( x^2 + x + 1) = 0
Phương trình có 2 nghiệm: x = 1 và x^2 + x + 1 =0 (phương trình bậc 2).
Bước 2: Kiểm tra giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
Để kiểm tra giá trị lớn nhất của hàm số, chúng ta có thể thay x = 1 vào hàm số:
y = - 1^4(1) - m = 3 - m
Điều kiện y < 10:
3 - m < 10
- m < 7
m > -7
Bước 3: Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Trong khoảng [-10;10], có 17 giá trị nguyên. Tuy nhiên, chúng ta chỉ quan tâm đến các giá trị m > -7.
Vậy, có 17 - 7 = 10 giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện y < 10.
Có bao nhiêu giá trị nguyên hàm của tham số m nhỏ hơn 10 để phương trình sau m + m + e x = e x có nghiệm thực?
A. 9
B. 8
C. 10
D. 7
Đáp án C
Đặt m + e x = a ; e x = b a ≥ 0 ; b > 0 ta có:
m + b = a m + a = b ⇔ m + b = a 2 m + a = b 2
⇔ m + b = a 2 b − a = a 2 − b 2 ⇔ m + b = a 2 a − b a + b + 1 = 0 ⇒ m = a 2 − b a = b
( Do a ≥ 0 ; b > 0 )
Khi đó m = b 2 − b b > 0
Do b 2 − b ≥ − 1 4 ∀ b > 0 nên phương trình có nghiệm khi m ≥ − 1 4
Do đó có 10 giá trị nguyên của m ∈ − 1 4 ; 10 thỏa mãn yêu cầu bài toán.
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x + 2 x + m đồng biến trên khoảng - ∞ ; - 10 ?
A. 7.
B. Vô số.
C. 9.
D. 8.

Vậy có 8 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án D
Có bao nhiêu giá trị nguyên của m ∈ (-10; 10) để hàm số y = f(x) = \(\left|3x^4-4x^3-6mx^2+12mx\right|\) có đúng 3 điểm cực trị
\(g\left(x\right)=3x^4-4x^3-6mx^2+12mx\)
\(g'\left(x\right)=12x^3-12x^2-12mx+12m=0\)
\(\Leftrightarrow12x^2\left(x-1\right)-12m\left(x-1\right)=0\)
\(\Leftrightarrow12\left(x^2-m\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x^2=m\end{matrix}\right.\)
Xét \(g\left(x\right)=0\Leftrightarrow x\left(3x^3-4x^2-6mx+12m\right)=0\)
- Nếu \(m=0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ \(\Rightarrow f\left(x\right)\) có 3 cực trị (thỏa mãn)
- Nếu \(m=\dfrac{1}{6}\Rightarrow g'\left(x\right)=0\) có 3 nghiệm bội lẻ, \(g\left(x\right)=0\) có 3 nghiệm pb nhưng chỉ có 1 nghiệm \(x=1\) trùng với \(g'\left(x\right)=0\) nên hàm có 5 cực trị (ktm)
- Nếu \(m=1\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ, \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (thỏa mãn)
- Nếu \(m< 0\Rightarrow g'\left(x\right)=0\) có 1 nghiệm bội lẻ \(x=1\)
Khi đó hàm có 3 cực trị khi \(g\left(x\right)=0\) có 2 nghiệm bội lẻ (hiển nhiên từ các TH này thì \(g\left(x\right)=0\) ko thể có nghiệm \(x=1\) do đã loại trừ từ TH \(m=\dfrac{1}{6}\))
\(\Leftrightarrow3x^3-4x^2-6mx+12m=0\) có đúng 1 nghiệm
\(\Leftrightarrow3x^3-4x^2=6m\left(x-2\right)\Leftrightarrow m=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) (do \(x=2\) ko là nghiệm)
Khảo sat \(h\left(x\right)=\dfrac{3x^3-4x^2}{6\left(x-2\right)}\) ta được \(y=m\) cắt \(y=h\left(x\right)\) tại đúng 1 điểm khi: \(\left[{}\begin{matrix}m< 0\\\dfrac{1}{6}< m< \dfrac{64}{9}\\\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
- Nếu \(m>0;m\ne\left\{\dfrac{1}{6};1\right\}\) \(\Rightarrow g'\left(x\right)=0\) có 3 nghiệm pb
Mà \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm bội lẻ \(x=0\)
\(\Rightarrow\) Hàm có 3 cực trị khi và chỉ khi:
TH1: \(3x^3-4x^2-6mx+12m=0\) vô nghiệm (vô lý do hàm bậc 3 luôn có nghiệm)
Th2: \(3x^3-4x^2-6mx+12m=0\) (1) có 3 nghiệm đều trùng với nghiệm của \(g'\left(x\right)=0\) (vô lý do \(m\ne\dfrac{1}{6}\) nên nếu (1) có nghiệm thì nó luôn có nghiệm khác 1)
Kết luận: \(\left[{}\begin{matrix}m=1\\m\le0\end{matrix}\right.\)
Có tất cả bao nhiêu giá trị nguyên của m
≥
10
sao cho đồ thị hàm số  có đúng một tiệm cận đứng?
có đúng một tiệm cận đứng?
A. 11
B. 10
C. 12
D. 9
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình \(x^2-2mx+m-10=0\) có hai nghiệm trái dấu
A.10 B.8 C.9 D.11
để pt có hai nghiệm trái dấu:
\(1.\left(m-10\right)< 0\\ =>m< 10\\ =>m=\left\{1;2;3;4;5;6;7;8;9\right\}\\ =>C\)
có bao nhiêu giá trị nguyên của tham số m để phương trinh \(15^x-5^x-3^x=\dfrac{m}{10}\) có 2 nghiệm thực phân biệt