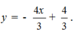Bài tập: Cho hàm số y=-\(\dfrac{1}{2}\)x2
a, Trên (P) lấy 2 điểm M và N lần lượt có hoành độ là -2 ; 1. Viết ptđt MN.
b, Xác định hàm số y=ax+b biết rằng đt (D) của nó song song với đt MN và chỉ cắt (P) tại 1 điểm.
Những câu hỏi liên quan
Cho hai hàm số y dfrac{1}{2}x^2 và y x2.a.Vẽ đồ thị của hai hàm số này trên cùng mặt phẳng tọa độ .b.Tìm tọa độ hai điểm A ; B có cùng hoành độ x 2 theo thứ tự nằm trên hai đồ thị .c.Gọi A’ và B’ lần lượt là các điểm đối xứng với A ; B qua trục tung Oy . Kiểm tra xem A’ ; B’ có lần lượt nằm trên hai đồ thị đó không ?
Đọc tiếp
Cho hai hàm số y = \(\dfrac{1}{2}x^2\) và y = x2.
a.Vẽ đồ thị của hai hàm số này trên cùng mặt phẳng tọa độ .
b.Tìm tọa độ hai điểm A ; B có cùng hoành độ x = 2 theo thứ tự nằm trên hai đồ thị .
c.Gọi A’ và B’ lần lượt là các điểm đối xứng với A ; B qua trục tung Oy . Kiểm tra xem A’ ; B’ có lần lượt nằm trên hai đồ thị đó không ?
a: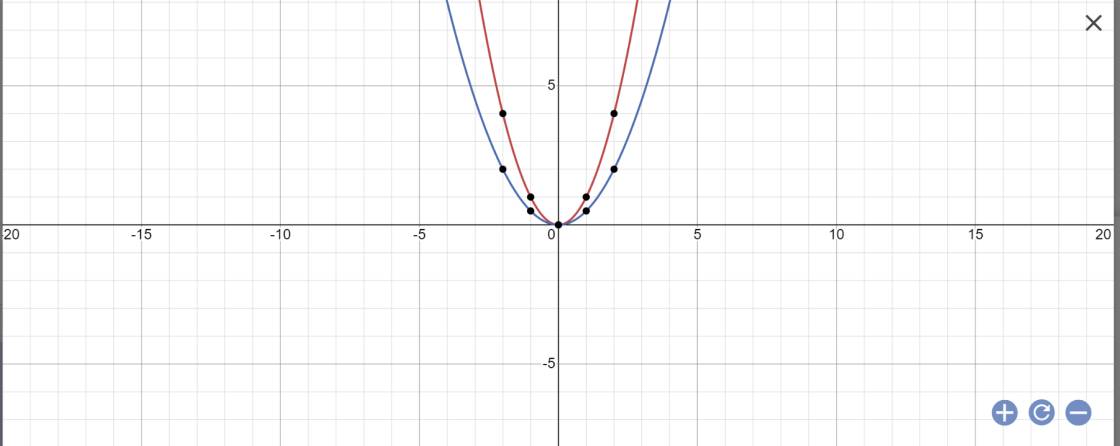 
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2
Đúng 2
Bình luận (0)
Cho hàm số y = 1/2 x^2 có đồ thị là (P).
a) Vẽ (P).
b) Trên (P) lấy hai điểm M và N có hoành độ lần lượt bằng –1 và 2.
Viết phương trình đường thẳng MN.
c) Tìm trên Oy điểm P sao cho MP + NP ngắn nhất.
a: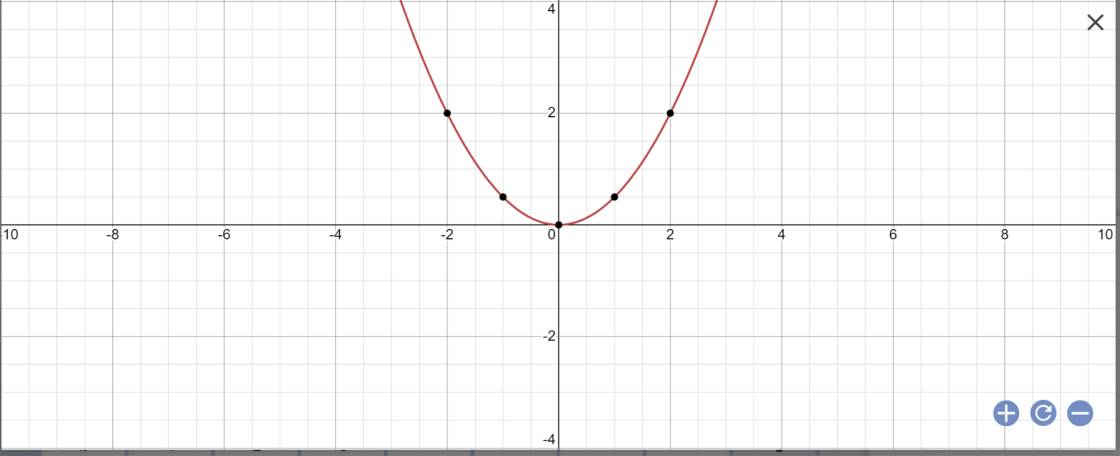 
b: f(-1)=1/2*(-1)^2=1/2
=>M(-1;1/2)
f(2)=1/2*2^2=2
=>N(2;2)
Gọi (d): y=ax+b là phương trình đường thẳng MN
Theo đề, ta có hệ:
-a+b=1/2 và 2a+b=2
=>a=1/2 và b=1
=>(d): y=1/2x+1
Đúng 0
Bình luận (0)
Bài 1: Cho hàm số yx2 có đồ thị (P) và hàm số y4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): yx2 Trên (P) lấy điểm A có hoành độ xA -2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y2x-5 có đồ thị là...
Đọc tiếp
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Bài 1: Cho hàm số yx2 có đồ thị (P) và hàm số y4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): yx2 Trên (P) lấy điểm A có hoành độ xA -2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y2x-5 có đồ thị là...
Đọc tiếp
Bài 1: Cho hàm số y=x2 có đồ thị (P) và hàm số y=4x+m có đồ thị (dm) Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó trung độ của một trong hai giao điểm đó bằng 1 Bài 2: Trong mặt phẳng Oxy cho parapol (P): y=x2 Trên (P) lấy điểm A có hoành độ xA =-2. Tìm tọa độ điểm M trên trục Ox sao cho |MA-MB| đạt giá trị lớn nhất, biết B(1;1) Bài 3: Tìm a và b để đường thẳng (d): y=(a-2)x+b có hệ số góc bằng 4 và đi qua điểm M(1;-3) Bài 4:Cho hàm số y=2x-5 có đồ thị là đường thẳng (d) a.Gọi A,B lần lượt là giao điểm của (d) với các trục tọa độ Ox,Oy. Tính tọa độ các điểm A,B và vẽ đường thẳng (d) trong mặt phẳng tọa độ Oxy b.Tính diện tích tam giác AOB HELP!!
Theo Cô si 4x+\frac{1}{4x}\ge2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014
Hơn nữa A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right. \Leftrightarrow x=\dfrac{1}{4} .
Vậy GTNN = 2014
Cho hàm số \(y=\dfrac{1}{2}x^2\)
1) Khảo sát và vẽ đồ thị (P) của hàm số.
2) Cho A B, là hai điểm nằm trên đồ thị (P) lần lượt có hoành độ là -1 và +2.
a) Viết phương trình đường thẳng d đi qua A và có hệ số góc bằng \(\dfrac{1}{2}\)
b) Chứng tỏ điểm B cũng nằm trên đường thẳng d.
Cho hàm số \(y=\dfrac{1}{2}x^2\)
1) Khảo sát và vẽ đồ thị (P) của hàm số.
2) Cho A B, là hai điểm nằm trên đồ thị (P) lần lượt có hoành độ là -1 và +2.
a) Viết phương trình đường thẳng d đi qua A và có hệ số góc bằng \(\dfrac{1}{2}\)
b) Chứng tỏ điểm B cũng nằm trên đường thẳng d.
Bài 7: Cho (P) y = \(\dfrac{1}{4}x^2\) và đường thẳng (d) đi qua hai điểm A và B trên (P) có hoành độ lần lượt là -2 và 4
1. Vẽ đồ thị (P) của hàm số trên
2. Viết Phương trình đường thẳng (d)
cho hàm số y=1/2x^2 có đồ thị là (P)
trên (P) lấy 2 điểm M và N có hoành độ lần lượt bằng -1 và 2 viết phương trình đường thẳng MN
tìm trên oy điểm P sao cho MP+NP ngắn nhất
29 tháng 6 2021 lúc 20:17
Cho hàm số y=x2 có đồ thị là (P) và hai điểm M,N thuộc (P) có hoành độ lần lượt là -1 và 2.
a, Viết phương trình đường thẳng đi qua hai điểm M,N
b, Vẽ đồ thị (P) trên hệ trục tọa độ Oxy và tìm tọa độ điểm E thuộc đoạn đường cong MN của đồ thị (P) sao cho ΔMNE có diện tích lớn nhất
a) Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Vậy: M(-1;1) và N(2;4)
Gọi (d):y=ax+b là ptđt đi qua hai điểm M và N
\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-3\\-a+b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
Vậy: (d): y=x+2
Đúng 1
Bình luận (0)
Cho hàm số
y
x
-
x
. Trên đồ thị của hàm số lấy hai điểm A và B hoành độ lần lượt là - 2 và 1. Phương trình đường thẳng AB là: A. B. C. D.
Đọc tiếp
Cho hàm số y = x - x . Trên đồ thị của hàm số lấy hai điểm A và B hoành độ lần lượt là - 2 và 1. Phương trình đường thẳng AB là:
A.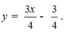 
B.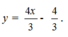 
C.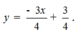 
D. 
