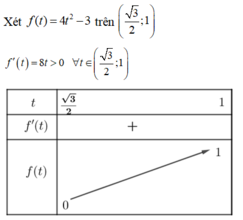
Dựa vào bảng biến thiên phương trình có nghiệm khi 0<m<1

Chọn D

Đáp án C

Ta có

  f ' x = − m s i n   x + 2 cos x − 3 ; y ' = 0 ⇔ − m s i n   x + 2 cos x = 3  

Phương trình này giải được với điều kiện là

m 2 + 2 2 ≥ 3 2 ⇔ m 2 ≥ 5 ⇔ m ∈ − ∞ ; − 5 ∪ 5 ; + ∞

Đáp án C

Ta có:  cos 2 3 x 1 + cos 6 x 2 = 4 cos 3 2 x − 3 cos 2 x + 1 2 và  cos 4 x = 2 cos 2 2 x − 1

Khi đó, phương trình đã cho 

⇔ 2 cos 2 2 x − 1 = 4 cos 3 2 x − 3 cos 2 x + 1 2 + 1 − cos 2 x 2 m

⇔ 4 cos 2 2 x − 2 = 4 cos 3 2 x − 3 cos 2 x + 1 + 1 − cos 2 x m

⇔ cos 2 x − 1 m = 4 cos 3 2 x − 4 cos 2 2 x − 3 cos 2 x + 3

Đặt t = cos 2 x , với x ∈ 0 ; π 12 → t ∈ 3 2 ; 1 do đó:  * ⇔ m 4 t 3 − 4 t 2 − 3 t + 3 t − 1 = 4 t 2 − 3

Xét hàm số f t = 4 t 2 − 3  trên khoảng  3 2 ; 1 → min f t = 0 max f t = 1

Vậy để phương trình m = f t có nghiệm khi và chỉ khi  m ∈ 0 ; 1

Đáp án C

Đặt t=cos2x, với , do đó (*) 

Đáp án C

Ta có c os 2 3 x = 1 + c os 6 x 2 = 4 c os 3 2 x − 3 c os 2 x + 1 2  

và  c os 4 x = 2 c os 2 2 x − 1

Khi đó, phương trình đã cho

⇔ 2 c os 2 2 x − 1 = 4 c os 3 2 x − 3 c os 2 x + 1 2 + 1 − c os 2 x 2 m

⇔ 4 c os 2 2 x − 2 = 4 c os 3 2 x − 3 c os 2 x + 1 + 1 − c os 2 x m ⇔ c os 2 x − 1 m = 4 c os 3 2 x − 4 c os 2 2 x − 3 c os 2 x + 3  

 Đặt t = c os 2 x ,  với x ∈ 0 ; π 12 → t ∈ 3 2 ; 1 ,  

do đó (*) ⇔ m = 4 t 3 − 4 t 2 − 3 t + 3 t − 1 = 4 t 2 − 3.  

Xét hàm số f t = 4 t 2 − 3  trên khoảng 3 2 ; 1 → min f t = 0 max f t = 1 .  

Vậy để phương trình m = f t  có nghiệm khi và chỉ khi  m ∈ 0 ; 1 .

1.

a, Phương trình có nghiệm khi: 

\(\left(m+2\right)^2+m^2\ge4\)

\(\Leftrightarrow m^2+4m+4+m^2\ge4\)

\(\Leftrightarrow2m^2+4m\ge0\)

\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)

b, Phương trình có nghiệm khi:

\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)

\(\Leftrightarrow2m^2+6m\le0\)

\(\Leftrightarrow-3\le m\le0\)

2.

a, Phương trình vô nghiệm khi:

\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)

\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)

\(\Leftrightarrow4m^2-7< 0\)

\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)

b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)

\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)

 Phương trình vô nghiệm khi:

\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)

\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)

\(\Leftrightarrow m^2-1>0\)

\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

1.

c, \(\left(m+2\right)sin2x+mcos^2x=m-2+msin^2x\)

\(\Leftrightarrow\left(m+2\right)sin2x+m\left(cos^2x-sin^2x\right)=m-2\)

\(\Leftrightarrow\left(m+2\right)sin2x+mcos2x=m-2\)

Phương trình vô nghiệm khi:

\(\left(m+2\right)^2+m^2< \left(m-2\right)^2\)

\(\Leftrightarrow m^2+4m+4+m^2< m^2-4m+4\)

\(\Leftrightarrow m^2+8m< 0\)

\(\Leftrightarrow-8\le m\le0\)

Đáp án B

PT

Đặt 

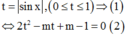
Để (1) có nghiệm thì (2) có nghiệm  có nghiệm

Suy ra 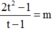có nghiệm 

Xét hàm số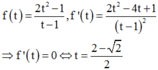 

Lập bảng biến thiên hàm số 

Đáp án B

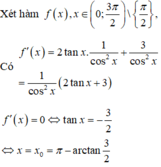
Bảng biến thiên

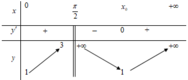
Từ BBt ta thấy, để phương trình có 3 nghiệm phân biệt trong khoảng 

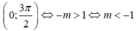
Cách 2 (casio): Thử bằng MTCT, sử dụng Mode 7

     + Thử với m = -2 ta thấy f(x) đổi dấu 3 lần nên có 3 nghiệm (loại đáp án C,D)

     + Thử với m = -1 ta thấy f(x) đổi dấu 2 lần nên có 2 nghiệm (loại A).