Tìm tọa độ của các vec tơ sau:
a) = 2
; b)
= -3
c) = 3
– 4
d)
= 0,2
+ √3
Trong khôn gian với hệ trục tọa độ O x y z , cho mặt cầu S : x 2 + ( y - 4 ) 2 + z 2 = 5 . Tìm tọa độ điểm A thuộc trục Oy, biết rằng ba mặt phẳng phân biệt qua A có các vec-tơ pháp tuyến lần lượt là các vec-tơ đơn vị của các trục tọa độ cắt mặt cầu theo thiết diện là ba hình tròn có tổng diện tích là 11 π
A. A ( 0 ; 2 ; 0 ) A ( 0 ; 6 ; 0 )
B. A ( 0 ; 0 ; 0 ) A ( 0 ; 8 ; 0 )
C. A ( 0 ; 0 ; 0 ) A ( 0 ; 6 ; 0 )
D. A ( 0 ; 2 ; 0 ) A ( 0 ; 8 ; 0 )
Đáp án A.
Mặt cầu (S) có tâm O ( 0 ; 4 ; 0 ) và bán kính R = 5 .Điểm A ∈ O y → A ( 0 ; b ; 0 ) . Khi đó ba mặt phẳng theo giả thiết đi qua A và có phương trình tổng quát lần lượt là α 1 : x = 0 , α 2 : y - b = 0 và α 3 : z = 0 .
Nhận thấy d I ; α 1 = d I ; α 2 = d I ; α 3 = 0 nên mặt cầu (S) cắt các mặt phẳng α 1 , α 3 theo giao tuyến là đường tròn lớn có tâm I, bán kính R = 5 . Tổng diện tích của hai hình tròn đó là S 1 + S 3 = 2 πR 2 = 10 π .
Suy ra mặt cầu (S) cắt α 2 theo giao tuyến là một đường tròn có diện tích là S 3 = 11 π - S 1 + S 2 = 11 π - 10 π = π . Bán kính đường tròn này là r = S 3 π = 1 .
→ d I , α 3 = R 2 - r 2 = 2 = 4 - b ⇔ b = 2 b = 6 . Vậy A 0 ; 2 ; 0 A ( 0 ; 6 ; 0 ) .
Trong khôn gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x 2 + y − 4 2 + z 2 = 5 . Tìm tọa độ điểm A thuộc trục Oy, biết rằng ba mặt phẳng phân biệt qua A có các vec-tơ pháp tuyến lần lượt là các vec-tơ đơn vị của các trục tọa độ cắt mặt cầu theo thiết diện là ba hình tròn có tổng diện tích là 11 π
A. A 0 ; 2 ; 0 A 0 ; 6 ; 0
B. A 0 ; 0 ; 0 A 0 ; 8 ; 0
C. A 0 ; 0 ; 0 A 0 ; 6 ; 0
D. A 0 ; 2 ; 0 A 0 ; 8 ; 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x + 2 y + z − 4 = 0 . Trong các vec tơ sau vec tơ nào không phải là véc tơ pháp tuyến của (P)?
A. n → = − 1 ; − 2 ; 1
B. n → = 1 ; 2 ; 1
C. n → = − 2 ; − 4 ; − 2
D. n → = 1 2 ; 1 ; 1 2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+2y+z-4=0. Trong các vec tơ sau vec tơ nào không phải là véc tơ pháp tuyến của (P)?
A. n → = - 1 ; - 2 ; 1
B. n → = 1 ; 2 ; 1
C. n → = - 2 ; - 4 ; - 2
D. n → = 1 2 ; 1 ; 1 2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-y-3z+2=0. Tìm 1 vec tơ pháp tuyến của (P)
A. (-4;2;6)
B. (2;-1;3)
C. (-2;1;-3)
D. (2;1;-3)
Trong mặt phằng tọa độ Oxy, cho điểm M’(4;2) Biết M’ là ảnh của M qua phép tịnh tiến theo vec tơ v → 1 ; 5 . Tìm tọa độ của điểm M
A. M − 3 ; − 5 .
B. M 3 ; 7 .
C. M − 5 ; 7 .
D. M − 5 ; − 3 .
Trong mặt phằng tọa độ Oxy, cho điểm M'(4;2) Biết M’ là ảnh của M qua phép tịnh tiến theo vec tơ v → 1 ; 5 . Tìm tọa độ của điểm M.
A. (-3;-5)
B. (3;7)
C. (-5;7)
D. (-5;-3)
Cho a → = (-1;2), b → = (2;-7) Tọa độ của vec tơ a → - b → là:
A.(6; -9)
B. (4; -5)
C.(-6; 9)
D.( -6; -9)
Trong mặt phẳng tọa độ, các mệnh đề sau đúng hay sai?
a) a→ (-3; 0) và i→ (1; 0) là hai vec tơ ngược hướng.
b) a→ (3; 4) và b→ (-3; -4) là hai vec tơ đối nhau
c) a→ (5; 3) và b→ (3; 5) là hai vec tơ đối nhau.
d) Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
a) Đúng
Giải thích: Nhận thấy a→ = -3.i→
Vì –3 < 0 nên a→ và i→ ngược hướng.
b) Đúng.
Giải thích:
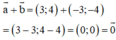
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.
c) Sai
Giải thích:
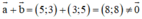
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.
d) Đúng
Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Trong mặt phẳng tọa độ Oxy cho A(5;2) ; B( 10; 8) . Tọa độ của vec tơ A B → là:
A.(2; 4)
B.( 5; 6)
C.(15; 10)
D.(50;6)