Trên đường tròn ( O, R ) lấy 3 cung liên tiếp \(\stackrel\frown{AB}=\frac{1}{6}\) ( O ) ; \(\stackrel\frown{BC}=\stackrel\frown{CD}=\frac{1}{3}\) ( O ). Gọi P là giao điểm của 2 dây AC và BD, Q là giao điểm của 2 tia BA và CD. Tính \(\widehat{APB}=\widehat{AQD}\)

Những câu hỏi liên quan
Cho đương tròn (O; R) tiếp tuyến Ax. Trên tia Ax lấy điểm M sao cho AM = \(\sqrt{3}R\) , OM cắt đương tròn ở N
a, Tính số đo góc ở tâm tạo bởi 2 bán kính OA và ON
b, Tính số đo cung nhỏ \(\stackrel\frown{AN}\) và cung lớn \(\stackrel\frown{AN}\)
a) Xét ΔOAM vuông tại A có
\(\tan\widehat{AOM}=\dfrac{AM}{AO}=\sqrt{3}\cdot\dfrac{OA}{OA}=\sqrt{3}\)
hay \(\widehat{AOM}=60^0\)
\(\Leftrightarrow\widehat{AON}=60^0\)
Vậy: Số đo góc ở tâm tạo bởi 2 bán kính OA và ON là 600
b) Xét (O) có
\(\stackrel\frown{AN}\) là cung chắn góc ở tâm \(\widehat{AON}\)(gt)
nên \(sđ\stackrel\frown{AN}=60^0\)
Số đo cung lớn AN là:
\(360^0-60^0=300^0\)
Đúng 1
Bình luận (0)
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính OCperp AB . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho sđstackrelfrown{CM}sđstackrelfrown{BN} . CMRa) stackrelfrown{AM}stackrelfrown{CN} và AMCNb) MNCACBGIẢI HỘ MK CÂU B) NHA
Đọc tiếp
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính \(OC\perp AB\) . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho \(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BN}\) . CMR
a) \(\stackrel\frown{AM}=\stackrel\frown{CN}\) và AM=CN
b) MN=CA=CB
GIẢI HỘ MK CÂU B) NHA![]()
b) Do \(\stackrel\frown{AM}=\stackrel\frown{CN}\) (theo câu a) => \(\widehat{AOM}=\widehat{CON}\)
Mà \(\widehat{AOM}+\widehat{MOC}=\widehat{AOC}=90^o\) => \(\widehat{NOC}+\widehat{MOC}=\widehat{MON}=90^o\)
Xét ΔOMN và ΔOAC có: \(\widehat{MON}=\widehat{AOC}=90^o\)
OA = OM (=bán kính nửa đường tròn)
OC = ON (=bán kính nửa đường tròn)
=> ΔOMN = ΔOAC (c.g.c) => MN = AC (2 cạnh tương ứng)
CMTT => ΔOMN = ΔOBC => MN = BC (2 cạnh tương ứng)
=> MN = AC = BC
Đúng 3
Bình luận (0)
cho nửa đường tròn ( O) đường kính AB . Vẽ bán kính OC\(\perp\)AB . Trên cung CA và CB lần lượt lấy các điểm M và N sao cho sđ\(\stackrel\frown{CM}=sđ\stackrel\frown{BN}\). CMR
a) \(\stackrel\frown{AM}=\stackrel\frown{CN}\) và AM=CN
b) MN=CA=CB
a) Xét (O) có
M là một điểm nằm trên cung \(\stackrel\frown{CA}\)(gt)
nên \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{MA}=sđ\stackrel\frown{CA}\)(1)
Xét (O) có
N là một điểm nằm trên cung \(\stackrel\frown{CB}\)(gt)
nên \(sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}=sđ\stackrel\frown{CB}\)(2)
Xét (O) có AB là đường kính(gt)
nên O là trung điểm của AB
Xét ΔCAB có
CO là đường cao ứng với cạnh AB(gt)
CO là đường trung tuyến ứng với cạnh AB(O là trung điểm của AB)
Do đó: ΔCAB cân tại C(Định lí tam giác cân)
⇒CA=CB
⇒\(sđ\stackrel\frown{CA}=sđ\stackrel\frown{CB}\)(3)
Từ (1), (2) và (3) suy ra \(sđ\stackrel\frown{CM}+sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}+sđ\stackrel\frown{NB}\)
mà \(sđ\stackrel\frown{CM}=sđ\stackrel\frown{BN}\)(gt)
nên \(sđ\stackrel\frown{AM}=sđ\stackrel\frown{CN}\)
hay \(\stackrel\frown{AM}=\stackrel\frown{CN}\)(đpcm)
Xét (O) có
AM là dây cung(A,M∈(O))
CN là dây cung(C,N∈(O))
\(\stackrel\frown{AM}=\stackrel\frown{CN}\)(cmt)
Do đó: AM=CN(Liên hệ giữa cung và dây)
Đúng 3
Bình luận (0)
Cho ΔAOB có \(\widehat{AOB}=110^o\) . Vẽ đường tròn (O, OA). Gọi C là 1 điểm trên đường tròn (O) biết sđ \(\stackrel\frown{AC}=40^0\) . Tính số đo cung nhỏ \(\stackrel\frown{BC}\) và cung lớn \(\stackrel\frown{BC}\)
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính OCperp AB . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho sđstackrelfrown{CM}sđstackrelfrown{BN} . cmr :a)cung AM cung CN và ANCNb)MNCACBLÀM GIÚP MÌNH CÂU B) Ạ
Đọc tiếp
cho nửa đường tròn (O) đường kính AB . Vẽ bán kính \(OC\perp AB\) . Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho sđ\(\stackrel\frown{CM}=sđ\stackrel\frown{BN}\) . cmr :
a)cung AM = cung CN và AN=CN
b)MN=CA=CB
LÀM GIÚP MÌNH CÂU B) Ạ![]()
![]()
Cho nửa đường tròn (O) đường kính Ae. Gọi B, C, D là 3 điểm trên nửa đường tròn sao cho \(\stackrel\frown{AC}=2\stackrel\frown{AB},\stackrel\frown{AD}=3\stackrel\frown{AB}\)
a, Chứng minh M là điểm chính giữa của \(\stackrel\frown{AD}và\stackrel\frown{BC}\) ( OM ⊥ AD)
b, Tứ giác ABCD là hình gì? Vì sao?
Cho hai đường tròn đồng tâm (O; R) và (O' R') với R > R'. Tiếp tuyến của đường tròn (O' R') tại A cắt đường tròn (O; R) tại B và C. Tia OA cắt đường tròn (O; R) tại E. So sánh \(\stackrel\frown{EB}\) và \(\stackrel\frown{EC}\)
Cần gấp !!!Trên nửa đường tròn tâm O đường kính AD lấy điểm C và B sao cho stackrelfrown{AC}stackrelfrown{CD},stackrelfrown{AB}stackrelfrown{BC} Gọi E là giao điểm của AB và DC,H là giao điểm của AC và BD, K là giao điểm của EH và AD,Tia HC cắt (D;DE) tại F,KC cắt EF tại M( Đã có tam giác ADE cân tại D, KHCD là tứ giác nội tiếp,KC//AE).CM: MB là tiếp tuyến của đường tròn đường kính ADCần gấp !!!!!!
Đọc tiếp
Cần gấp !!!
Trên nửa đường tròn tâm O đường kính AD lấy điểm C và B sao cho \(\stackrel\frown{AC}>\stackrel\frown{CD}\),\(\stackrel\frown{AB}=\stackrel\frown{BC}\) Gọi E là giao điểm của AB và DC,H là giao điểm của AC và BD, K là giao điểm của EH và AD,Tia HC cắt (D;DE) tại F,KC cắt EF tại M( Đã có tam giác ADE cân tại D, KHCD là tứ giác nội tiếp,KC//AE).CM: MB là tiếp tuyến của đường tròn đường kính AD
Cần gấp !!!!!!
c, Do KC // AE
\(\Rightarrow\)CM // AE
Ta có DF = DA = DE ( \(\Delta DAE.cân.ở.D\) )
\(\Rightarrow\Delta ADF\) cân ở D mà DC là đường cao ứng với đáy
\(\Rightarrow\) AC = CF
Mà CM // AE
\(\Rightarrow\) CM là đường TB
\(\Rightarrow ME=MF\)
\(\Delta AED\) cân ở D. BD là đường cao
\(\Rightarrow\) BD là trung tuyến
\(\Rightarrow\) BA = BE
mà ME = MF
\(\Rightarrow\) BM là đường TB ứng vớ cạnh đáy AF
\(\Rightarrow\) BM // AF ; BM // AC
Vì \(\stackrel\frown{BA}=\stackrel\frown{BC}\Rightarrow BO\perp AC\)
Mà BM // AC
\(\Rightarrow BO\perp BM\)
\(\Rightarrow\) BM là tiếp tuyến đường tròn tâm O đường kính AD
Đúng 1
Bình luận (1)
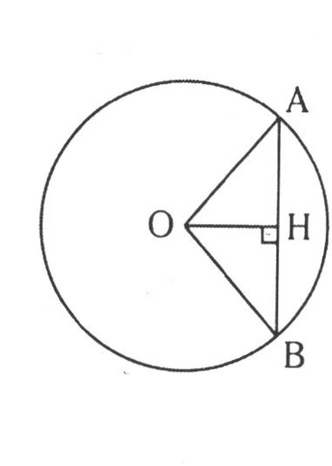
Cho đường tròn (O;R), vẽ dây AB sao cho sđ \(\stackrel\frown{AB}\) nhỏ = \(\dfrac{1}{2}\) sđ\(\stackrel\frown{AB}\) lớn. Tính diện tích \(\Delta\)AOB
Tham khảo ha:
https://hoidap247.com/cau-hoi/522596
Đúng 0
Bình luận (0)
\(Ta.có:\\ Sđ\stackrel\frown{AB}_{lớn}+Sđ\stackrel\frown{AB}_{nhỏ}=360^0\\ mà.Sđ\stackrel\frown{AB}_{lớn}=2Sđ\stackrel\frown{AB}_{nhỏ}\\ Sđ\stackrel\frown{AB}_{nhỏ}=Sđ\widehat{AOB}\\ nên.Sđ\stackrel\frown{AB}_{nhỏ}=120^0\\ Kẻ.OH\perp AB\Rightarrow\widehat{AOH}=60^0\\ \Rightarrow\Delta AOH.là.nửa.\Deltađều\\ \Rightarrow OH=\dfrac{OA}{2}=\dfrac{R}{2}.và.AH=\dfrac{R\sqrt{3}}{2}\)
\(Vì.OH\perp AB.nên.AB=2AH=2.\dfrac{R\sqrt{3}}{2}=R\sqrt{3}\\ Vậy.S_{OAB}=\dfrac{1}{2}AB.OH=\dfrac{R^2\sqrt{3}}{4}\)
Đúng 0
Bình luận (0)