Cho (d1): 2x + 3y - 5 = 0; (d2): 2x + 3y + 1 = 0. Viết phương trình (d) đối xứng (d1) qua (d2)

Những câu hỏi liên quan
cho đt (d): 2x-3y-1=0, và (d1): -2x+3y+2=0
a) chứng minh (d) song song với (d1)
b) tính khoảng cách (d) và (d1)
D1: 2x+3y-5=0 và d2: 4x-3y-1=0
Trong mặt phẳng
v
→
(
−
2
;
1
)
cho, đường thẳng d có phương trình 2x − 3y + 3 0, đường thẳng
d
1
có phương trình
2
x
−
3
y
−
5
0
.
Tìm t...
Đọc tiếp
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Tìm tọa độ của w → có giá vuông góc với đường thẳng d để d 1 là ảnh của d qua T w →
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của
d
2
là 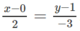 .
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
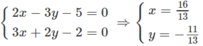
Từ đó suy ra
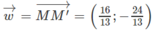
Đúng 0
Bình luận (0)
Trong mặt phẳng
v
→
(
−
2
;
1
)
cho, đường thẳng d có phương trình 2x − 3y + 3 0, đường thẳng
d
1
có phương trình
2
x
−
3
y
−
5
0...
Đọc tiếp
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Viết phương trình của đường thẳng d’ là ảnh của d qua T v → .
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Khi đó M′ = T v → ( M ) = (0 − 2; 1 + 1) = (−2; 2) thuộc d'.
Vì d' song song với d nên phương trình của nó có dạng 2x − 3y + C = 0.
Do M' ∈ d′ nên 2.(−2) − 3.2 + C = 0. Từ đó suy ra C = 10 .
Do đó d' có phương trình 2x − 3y + 10 = 0.
Đúng 0
Bình luận (0)
Cho 3 đường thẳng d1:x-2y+5=0, d2: 2x-3y+7=0, d3: 3x+4y-1=0. Viết phương trình đường thẳng d đi qua giao điểm của d1 và d2, và song song với d3.
Giao điểm A của d1 và d2 là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-2y+5=0\\2x-3y+7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow A\left(1;3\right)\)
Do \(d//d_3\Rightarrow d\) nhận \(\overrightarrow{n_d}=\left(3;4\right)\) là 1 vtpt
Phương trình d:
\(3\left(x-1\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-15=0\)
Đúng 0
Bình luận (0)
Cho hai đường thẳng d1 2x - 3y +1 = 0 và d2 -4x + 6y -3 = 0
viết đường thẳng // với d1 và d2
Đường thẳng song song với d1 và d2 là:
(d3): 2x - 3y + c (với c khác 1 và c khác 1,5)
Đúng 0
Bình luận (0)
Cho hai đường thẳng
d
1
:
6
x
−
3
y
+
4
0
,
d
2
:
2
x
−
y
+
3
0
. Bán kính đường tròn tiếp xúc với hai đường thẳng d1;d2 là A.
3
5
B.
3
5...
Đọc tiếp
Cho hai đường thẳng d 1 : 6 x − 3 y + 4 = 0 , d 2 : 2 x − y + 3 = 0 . Bán kính đường tròn tiếp xúc với hai đường thẳng d1;d2 là
A. 3 5
B. 3 5
C. 5 6
D. 5 3
ĐÁP ÁN C
Ta có: 6 2 = − 3 − 1 ≠ 4 3 nên d1 // d2.
Ta có: d 2 : 2 x − y + 3 = 0 ⇔ 6 x − 3 y + 9 = 0
Do d1 // d2. nên khoảng cách hai đường thẳng d1và d2 chính là đường kính của đường tròn.
Suy ra, bán kính đường tròn tiếp xúc với hai đường thẳng d1;d2 là
R = 1 2 d d 1 , d 2 = 1 2 9 − 4 6 2 + − 3 2 = 5 6
Đúng 0
Bình luận (0)
Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng
d
1
:
2
x
+
3
y
+
1
0
và
d
2
:
x
-
y
-
2
0
Có bao nhiêu phép tịnh tiến biến...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho hai đường thẳng d 1 : 2 x + 3 y + 1 = 0
và d 2 : x - y - 2 = 0 Có bao nhiêu phép tịnh tiến biến d 1 thành d 2
A.Vô số
B.4
C.1
D.0
Chọn D.
Vì d 1 không song song hoặc trùng với d 2 nên không tồn tại phép tịnh tiến nào biến d 1 thành d 2
Đúng 0
Bình luận (0)












