Cho tam giác MNP có \(\widehat{M}=30^o;\widehat{N}=20^o\)trên MN lấy D sao cho MD=NP. Tính \(\widehat{NPD}\)

Những câu hỏi liên quan
Cho tam giác MNP có \(\widehat{M}=30^o;\widehat{N}=20^o\)trên MN lấy D sao cho MD=NP. Tính \(\widehat{NPD}\)
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
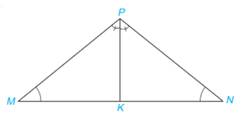
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Đúng 0
Bình luận (0)
a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.
b) Cho tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.
a)
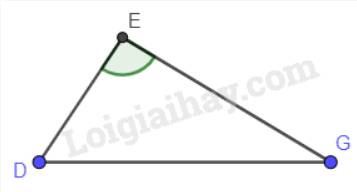
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.
Vậy DE < DG.
b)

Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ - 56^\circ - 65^\circ = 59^\circ \).
Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).
Đúng 0
Bình luận (0)
Cho tam giác MNP có \(\widehat{M}\) = 25o. \(\widehat{N}\) = 80o thì góc ngoài của tam giác tại đỉnh P có số đo bằng?
Cho hai tam giác bằng nhau: Tam giác ABC và tam giác có ba đỉnh là M, N, P. Biết widehat{A}widehat{N}; widehat{C}widehat{M}. Hệ thức bằng nhau giữa hai tam giác theo thứ tự đỉnh tương ứng là:A. △ABC △MNP B. △ABC △NPMC. △BAC △PMN D. △CAB △MNP
Đọc tiếp
Cho hai tam giác bằng nhau: Tam giác ABC và tam giác có ba đỉnh là M, N, P. Biết \(\widehat{A}=\widehat{N}\); \(\widehat{C}=\widehat{M}\). Hệ thức bằng nhau giữa hai tam giác theo thứ tự đỉnh tương ứng là:
A. △ABC = △MNP B. △ABC = △NPM
C. △BAC = △PMN D. △CAB = △MNP
Xem thêm câu trả lời
Cho tam giác MNP có \(\widehat M = 47^\circ ;\widehat N = 53^\circ \). Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.
Áp dụng định lí tổng ba góc trong một tam giác trong tam giác MNP, có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\ \Rightarrow 47^\circ + 53^\circ + \widehat P = 180^\circ \\ \Rightarrow \widehat P = 180^\circ - 47^\circ - 53^\circ = 80^\circ \\ \Rightarrow \widehat M < \widehat N < \widehat P(47^\circ < 53^\circ < 80^\circ )\end{array}\)
\( \Rightarrow \) NP < MP < MN ( cạnh đối diện với góc lớn hơn thì lớn hơn)
Vậy các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn là NP, MP, MN.
Đúng 1
Bình luận (0)
Cho hai tam giác ABC và MNP có widehat{C}widehat{P}90^o,ABMNCP90o,ABMN và widehat{B}widehat{N}.BN. Biết AB 7cm. Tìm MN.
MN cm.
Đọc tiếp
Cho hai tam giác ABC và MNP có và Biết AB = 7cm. Tìm MN.
MN = cm.
Cho tam giác ABC có \(BC=2cm\), \(\widehat{A}=105^o\), \(\widehat{C}=30^o\). Tính diện tích tam giác ABC.
Có \(\widehat{B}=180^0-105^0-30^0=45^0\)
Kẻ AH vuông góc với BC
\(\Rightarrow\Delta ABH\) là tam giác vuông cân tại A
\(\Rightarrow AH=BH\)
Có \(tanC=\dfrac{AH}{HC}\Leftrightarrow HC=\dfrac{AH}{tan30^0}=\sqrt{3}AH\)
\(\Rightarrow BH+CH=AH+\sqrt{3}AH\Leftrightarrow BC=\left(1+\sqrt{3}\right)AH\)\(\Leftrightarrow AH=\dfrac{BC}{1+\sqrt{3}}=\dfrac{2}{1+\sqrt{3}}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2}{1+\sqrt{3}}.2=\dfrac{2}{1+\sqrt{3}}\) (cm2)
Vậy...
Đúng 3
Bình luận (0)
Cho \(\Delta MNP\)có \(\widehat{M}=30^o\); \(\widehat{N}=30^o\). Trên cạnh MN lấy D sao cho MD=NP. Tính \(\widehat{NPD}\)























