Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = -2.
\(\begin{array}{l}P = 5{x^4} - 3{x^3}y + 2x{y^3} - {x^3}y + 2{y^4} - 7{x^2}{y^2} - 2x{y^3};\\Q = {x^3} + {x^2}y + x{y^2} - {x^2}y - x{y^2} - {x^3}.\end{array}\)
Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = -2.
\(\begin{array}{l}P = 5{x^4} - 3{x^3}y + 2x{y^3} - {x^3}y + 2{y^4} - 7{x^2}{y^2} - 2x{y^3};\\Q = {x^3} + {x^2}y + x{y^2} - {x^2}y - x{y^2} - {x^3}.\end{array}\)
Cho hai đa thức:
\(A = 7xy{z^2} - 5x{y^2}z + 3{x^2}yz - xyz + 1;B = 7{x^2}yz - 5x{y^2}z + 3xy{z^2} - 2.\)
a) Tìm đa thức C sao cho A-C=B;
b) Tìm đa thức D sao cho A+D=B;
c) Tìm đa thức E sao cho E-A=B;
Thảo luận (1)Hướng dẫn giảia)
\(\begin{array}{l}A - C = B\\ \Rightarrow C = A - B \\= 7xy{z^2} - 5x{y^2}z + 3{x^2}yz - xyz + 1 - \left( {7{x^2}yz - 5x{y^2}z + 3xy{z^2} - 2} \right)\\ = 7xy{z^2} - 5x{y^2}z + 3{x^2}yz - xyz + 1 - 7{x^2}yz + 5x{y^2}z - 3xy{z^2} + 2\\ = \left( {7xy{z^2} - 3xy{z^2}} \right) + \left( { - 5x{y^2}z + 5x{y^2}z} \right) + \left( {3{x^2}yz - 7{x^2}yz} \right) - xyz + \left( {1 + 2} \right)\\ = 4xy{z^2} - 4{x^2}yz - xyz + 3\end{array}\)
b)
\(\begin{array}{l}A + D = B\\ \Rightarrow D = B - A \\= - \left( {A - B} \right) = - C \\= - 4xy{z^2} + 4{x^2}yz + xyz - 3.\end{array}\)
c)
\(\begin{array}{l}E - A = B\\ \Rightarrow E = A + B = A \\= 7xy{z^2} - 5x{y^2}z + 3{x^2}yz - xyz + 1 + 7{x^2}yz - 5x{y^2}z + 3xy{z^2} - 2\\ = \left( {7xy{z^2} + 3xy{z^2}} \right) + \left( { - 5x{y^2}z - 5x{y^2}z} \right) + \left( {3{x^2}yz + 7{x^2}yz} \right) - xyz + \left( {1 - 2} \right)\\ = 10xy{z^2} - 10x{y^2}z + 10{x^2}yz - xyz - 1\end{array}\)
(Trả lời bởi Hà Quang Minh)
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimet và y centimet. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimet) như Hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
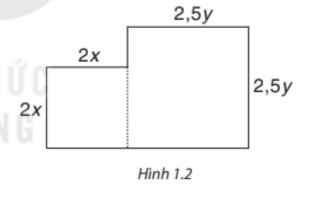
Thảo luận (1)Hướng dẫn giảiDiện tích hai hình vuông là: \(2x.2x + 2,5y.2,5y = 4{x^2} + 6.25{y^2}\)
Diện tích hai hình tròn là: \({\pi .{x^2} + \pi .{y^2}}\)
Diện tích phần còn lại của miếng bìa là:
\(\begin{array}{l}S = 4{x^2} + 6.25{y^2} - \pi .{x^2} - \pi .{y^2}\\ = \left( {4 - \pi } \right){x^2} + \left( {6,25 - \pi } \right){y^2}\end{array}\)
Biểu thức này là một đa thức, có bậc là 2.
(Trả lời bởi Hà Quang Minh)
Cho ba đa thức:
\(M = 3{x^3} - 4{x^2}y + 3x - y;N = 5xy - 3x + 2;P = 3{x^3} + 2{x^2}y + 7x - 1.\)
Tính M+N-P và M-N-P.
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}M + N - P = 3{x^3} - 4{x^2}y + 3x - y + 5xy - 3x + 2 - \left( {3{x^3} + 2{x^2}y + 7x - 1} \right)\\ = 3{x^3} - 4{x^2}y + 3x - y + 5xy - 3x + 2 - 3{x^3} - 2{x^2}y - 7x + 1\\ = \left( {3{x^3} - 3{x^3}} \right) + \left( { - 4{x^2}y - 2{x^2}y} \right) + 5xy + \left( {3x - 3x - 7x} \right) - y + \left( {2 + 1} \right)\\ = - 6{x^2}y + 5xy - 7x - y + 3\\M - N - P = 3{x^3} - 4{x^2}y + 3x - y - \left( {5xy - 3x + 2} \right) - \left( {3{x^3} + 2{x^2}y + 7x - 1} \right)\\ = 3{x^3} - 4{x^2}y + 3x - y - 5xy + 3x - 2 - 3{x^3} - 2{x^2}y - 7x + 1\\ = \left( {3{x^3} - 3{x^3}} \right) + \left( { - 4{x^2}y - 2{x^2}y} \right) - 5xy + \left( {3x + 3x - 7x} \right) - y + \left( { - 2 + 1} \right)\\ = - 6{x^2}y - 5xy - x - y - 1\end{array}\)
(Trả lời bởi Hà Quang Minh)