Cho \(A = [-2;3],\;\,B = (1; + \infty )\). Xác định các tập hợp sau:
\(\;A \cap B; B \backslash A \) và \({C_\mathbb{R}}B\)
Cho \(A = [-2;3],\;\,B = (1; + \infty )\). Xác định các tập hợp sau:
\(\;A \cap B; B \backslash A \) và \({C_\mathbb{R}}B\)
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - \infty ;1) \cap (0; + \infty )\)
b) \((4;7] \cup ( - 1;5)\)
c) \((4;7]\;{\rm{\backslash }}\;( - 3;5]\)
Thảo luận (1)Hướng dẫn giảiTham khảo:
a) Ta có:
Giao của hai tập hợp là \(( - \infty ;1) \cap (0; + \infty ) = (0;1)\)
b) Ta có:
Hợp của hai tập hợp là \((4;7] \cup ( - 1;5) = ( - 1;7]\)
c) Ta có:
Hiệu của tập hợp \((4;7]\) và tập hợp \(( - 3;5]\) là \((4;7]\;{\rm{\backslash }}\;( - 3;5] = (5;7]\)
(Trả lời bởi Kiều Sơn Tùng)
Cho tập hợp A,B được mình họa bằng biểu đồ Ven như hình bên. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
A. \(A \cap B\)
B. \(A\;{\rm{\backslash }}\;B\)
C. \(A \cup B\)
D. \(B\;{\rm{\backslash }}\;A\)
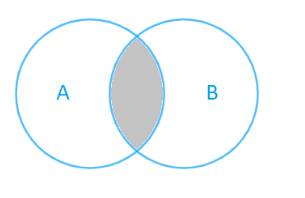
Thảo luận (3)Hướng dẫn giảiPhần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là \(A \cap B\)
Chọn đáp án A
(Trả lời bởi Hà Quang Minh)
Cho \(A = \left\{ {x \in \mathbb{N}|\;x < 7} \right\},\) \(\,B = \left\{ {1;2;3;6;7;8} \right\}\). Xác định các tập hợp sau:
\(A \cup B,\;A \cap B,\;A\,{\rm{\backslash }}\,B\)
Thảo luận (1)Hướng dẫn giải\(A = \left\{ {0;1;2;3;4;5;6} \right\}\)
\(\,B = \left\{ {1;2;3;6;7;8} \right\}\)
Vậy
\(A \cap B = \left\{ {1;2;3;6} \right\}\)
\(A \cup B = \left\{ {0;1;2;3;4;5;6;7;8} \right\} = \left\{ {x \in \mathbb{N}|\;x < 9} \right\}\)
\(A\;{\rm{\backslash }}\;B = \left\{ {0;4;5} \right\}\)
(Trả lời bởi Hà Quang Minh)
Biểu diễn các tập hợp sau bằng biểu đồ Ven:
a) \(A = \left\{ {0;1;2;3} \right\}\)
b) B = {Lan; Huệ; Trang}
Thảo luận (1)Hướng dẫn giảiTham khảo:
a) \(A = \left\{ {0;1;2;3} \right\}\). Biểu đồ Ven:
b) B = {Lan; Huệ; Trang}. Biểu đồ Ven:
(Trả lời bởi Kiều Sơn Tùng)
Cho tập hợp A = {a;b;c}. Tập A có bao nhiêu tập con?
A. 4
B. 6
C. 8
D. 10
Thảo luận (3)Hướng dẫn giảiTập A có các tập con là:
+) tập hợp rỗng.
+) 3 tập con có 1 phần tử là: {a}, {b}, {c}
+) 3 tập con có 2 phần tử là: {a;b}, {b;c}, {c;a}
+) 1 tập con có 3 phần tử: {a;b;c} (là tập A)
Vậy tập A có 1+3+3+1=8 tập hợp con.
Chọn C.
Chú ý khi giải
+ Khi tính số tập hợp con, mọi tập A luôn có 2 tập con là tập \(\emptyset \) và chính nó.
+ Số tập hợp con của tập hợp A có n phần tử là: \({2^n}\)
(Trả lời bởi Hà Quang Minh)
Cho định lí: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây là đúng?
A. Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
B. Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau
C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau
D. Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau
Thảo luận (3)Hướng dẫn giảiTừ định lí: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”, ta có:
"Hai tam giác bằng nhau là điều kiện đủ để chúng có diện tích bằng nhau"
"Hai tam giác có diện tích bằng nhau là điều kiện cần để chúng bằng nhau"
=> A và C sai, D đúng.
B. "Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau"
Dễ thấy Q:"diện tích bằng nhau" không suy ra P:"hai tam giác đó bằng nhau".
=> \(Q \not{\Rightarrow}P\) sai => mệnh đề \(P \Leftrightarrow Q\) sai
=> B sai
Chọn D.
(Trả lời bởi Hà Quang Minh)
Câu nào sau đây không là mệnh đề?
A. Tam giác đều là tam giác có ba cạnh bằng nhau.
B. \(3\;\, < 1\)
C. \(4 - 5 = 1\)
D. Bạn học giỏi quá!
Thảo luận (1)Hướng dẫn giảiA. “Tam giác đều là tam giác có ba cạnh bằng nhau.” Là một mệnh đề đúng
B. “\(3\;\, < 1\)” là một mệnh đề sai
C. “\(4 - 5 = 1\)” là một mệnh đề sai
D. “Bạn học giỏi quá!” là câu cảm thán, không xác định được tính đúng sai nên không là một mệnh đề.
Chọn D.
(Trả lời bởi Hà Quang Minh)
Mệnh đề nào sau đây là đúng?
A. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\)
B. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\)
C. \(\forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\)
D. \(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\)
Thảo luận (2)Hướng dẫn giảiA. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\)
Sai, chẳng hạn với \(x = - 2\) thì \({x^2} = 4 > 1\) nhưng \(x = - 2 < - 1\).
B. \(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\)
Sai, chẳng hạn với \(x = - 2\) thì \({x^2} = 4 > 1\) nhưng \(x = - 2 < 1\).
C. \(\forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\)
Sai, chẳng hạn với \(x = 0 > - 1\) nhưng \({x^2} = 0 < 1\)
D. \(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\)
Đúng.
Chọn đáp án D
(Trả lời bởi Hà Quang Minh)
Phần không bị gạch trên trục số dưới đây biểu diễn tập hợp số nào?

Thảo luận (2)Hướng dẫn giảiTa có:
Biểu diễn khoảng \(\left( { - \infty ; - 2} \right)\)
Biểu diễn nửa khoảng \([5; + \infty )\)
Vậy phần không bị gạch trên trục số là \(\left( { - \infty ; - 2} \right) \cup [5; + \infty )\)
(Trả lời bởi Kiều Sơn Tùng)