Cho P(A) = \(\dfrac{2}{5}\); P(B | A) = \(\dfrac{1}{3}\); P(B | \(\overline{A}\)) = \(\dfrac{1}{4}\).
Giá trị P(AB) là:
A. \(\dfrac{2}{5}\). B. \(\dfrac{3}{16}\). C. \(\dfrac{1}{5}\). D. \(\dfrac{4}{15}\).
Cho P(A) = \(\dfrac{2}{5}\); P(B | A) = \(\dfrac{1}{3}\); P(B | \(\overline{A}\)) = \(\dfrac{1}{4}\).
Giá trị P(B\(\overline{A}\)) là:
A. \(\dfrac{1}{7}\). B. \(\dfrac{4}{19}\). C. \(\dfrac{4}{21}\). D. \(\dfrac{3}{20}\).
Thảo luận (1)Hướng dẫn giải\(P\left( {B\overline A } \right) = P\left( {\overline A } \right).P\left( {B|\overline A } \right) = \left( {1 - \frac{2}{5}} \right).\frac{1}{4} = \frac{3}{{20}}\)
Chọn D
(Trả lời bởi datcoder)
Cho P(A) = \(\dfrac{2}{5}\); P(B | A) = \(\dfrac{1}{3}\); P(B | \(\overline{A}\)) = \(\dfrac{1}{4}\).
Giá trị P(B) là:
A. \(\dfrac{19}{60}\). B. \(\dfrac{17}{60}\). C. \(\dfrac{9}{20}\). D. \(\dfrac{7}{30}\).
Thảo luận (1)Hướng dẫn giảiVì AB và \(\overline A B\) là hai biến cố xung khắc và \(\overline A B \cup AB = B\)
Do đó, \(P\left( B \right) = P\left( {AB} \right) + P\left( {\overline A B} \right) = \frac{2}{{15}} + \frac{3}{{20}} = \frac{{17}}{{60}}\)
Chọn B
(Trả lời bởi datcoder)
Bạn An có một túi gồm một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 6 chiếc kẹo sô cô la đen, còn lại 4 chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên 1 chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp 1 chiếc kẹo nữa trong túi và cũng đưa cho Bình.
Xác suất để Bình nhận được 2 chiếc kẹo sô cô la đen là
A. \(\dfrac{1}{3}\). B. \(\dfrac{1}{4}\). C. \(\dfrac{2}{5}\). D. \(\dfrac{3}{7}\).
Thảo luận (1)Hướng dẫn giảiBình nhận được 2 chiếc kẹo sô cô la đen khi cả hai lần An đều lấy được 2 chiếc sô cô la đen. Khi đó, xác suất để Bình nhận được 2 chiếc kẹo sô cô la đen là: \(\frac{6}{{10}}.\frac{5}{9} = \frac{1}{3}\)
Chọn A
(Trả lời bởi datcoder)
Bạn An có một túi gồm một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 6 chiếc kẹo sô cô la đen, còn lại 4 chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên 1 chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp 1 chiếc kẹo nữa trong túi và cũng đưa cho Bình.
Xác suất để Bình nhận được 2 chiếc kẹo sô cô la trắng là
A. \(\dfrac{1}{5}\). B. \(\dfrac{2}{15}\). C. \(\dfrac{1}{4}\). D. \(\dfrac{4}{17}\).
Thảo luận (1)Hướng dẫn giảiBình nhận được 2 chiếc kẹo sô cô la trắng khi cả hai lần An đều lấy được 2 chiếc sô cô la trắng. Khi đó, xác suất để Bình nhận được 2 chiếc kẹo sô cô la trắng là: \(\frac{4}{{10}}.\frac{3}{9} = \frac{2}{{15}}\)
Chọn B
(Trả lời bởi datcoder)
Bạn An có một túi gồm một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 6 chiếc kẹo sô cô la đen, còn lại 4 chiếc kẹo sô cô la trắng. An lấy ngẫu nhiên 1 chiếc kẹo trong túi để cho Bình, rồi lại lấy ngẫu nhiên tiếp 1 chiếc kẹo nữa trong túi và cũng đưa cho Bình.
Xác suất để Bình nhận được chiếc kẹo sô cô la đen ở lần thứ nhất, chiếc kẹo sô cô la trắng ở lần thứ hai là
A. \(\dfrac{1}{5}\). B. \(\dfrac{3}{16}\). C. \(\dfrac{1}{4}\). D. \(\dfrac{4}{17}\).
Thảo luận (1)Hướng dẫn giảiXác suất để Bình nhận được chiếc kẹo sô cô la đen ở lần thứ nhất, chiếc kẹo sô cô la trắng ở lần thứ hai là: \(\frac{6}{{10}}.\frac{4}{9} = \frac{4}{{15}}\).
Không có đáp án
(Trả lời bởi datcoder)
Để thử nghiệm tác dụng điều trị bệnh mất ngủ của hai loại thuốc X và thuốc Y, người ta tiến hành thử nghiệm trên 4 000 người bệnh tình nguyện. Kết quả được cho trong bảng thống kê 2 × 2 sau:
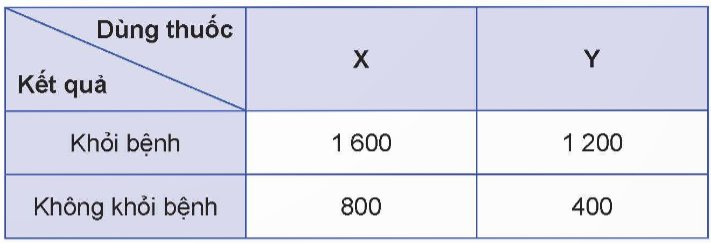
Chọn ngẫu nhiên 1 người bệnh tham gia tình nguyện thử nghiệm thuốc.
a) Tính xác suất để người đó khỏi bệnh nếu biết người bệnh đó uống thuốc X.
b) Tính xác suất để người bệnh đó uống thuốc Y, biết rằng người đó khỏi bệnh.
Thảo luận (1)Hướng dẫn giảiKhông gian mẫu \(\Omega \) là tập hợp gồm 4 000 bệnh nhân thử nghiệm nên \(n\left( \Omega \right) = 4000\)
a) Gọi A là biến cố: “Người đó uống thuốc X”, B là biến cố “Người đó khỏi bệnh”.
Khi đó biến cố AB là: “Người đó uống thuốc X và khỏi bệnh”
Ta có: \(1600 + 800 = 2400\) người uống thuốc X nên \(n\left( A \right) = 2400\). Do đó, \(P\left( A \right) = \frac{{2400}}{{4000}}\)
Trong số những người uống thuốc X, có 1 600 người khỏi bệnh nên \(n\left( {AB} \right) = 1\;600\)
Do đó, \(P\left( {AB} \right) = \frac{{1600}}{{4000}}\). Vậy \(P\left( {B|A} \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{{1600}}{{2400}} = \frac{2}{3}\)
b) Gọi A là biến cố: “Người đó uống thuốc Y”, B là biến cố “Người đó khỏi bệnh”
Khi đó biến cố AB là: “Người đó uống thuốc Y và khỏi bệnh”.
Ta có: \(1200 + 1600 = 2800\) khỏi bệnh nên \(n\left( B \right) = 2800\). Do đó, \(P\left( B \right) = \frac{{2800}}{{4000}}\)
Trong số những người khỏi bệnh, có 1200 người uống thuốc Y nên \(n\left( {AB} \right) = 1200\)
Do đó, \(P\left( {AB} \right) = \frac{{1200}}{{2800}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{1200}}{{2800}} = \frac{3}{7}\)
(Trả lời bởi datcoder)
Một nhóm có 25 học sinh, trong đó có 14 em học khá môn Toán, 16 em học khá môn Vật lí, 1 em không học khá cả hai môn Toán và môn Vật lí. Chọn ngẫu nhiên một học sinh trong số đó. Tính xác suất để học sinh đó:
a) Học khá môn Toán, đồng thời học khá môn Vật lí;
b) Học khá môn Toán, nhưng không học khá môn Vật lí;
c) Học khá môn Toán, biết rằng học sinh đó học khá môn Vật lí.
Thảo luận (1)Hướng dẫn giảiCó 25 học sinh trong một nhóm nên số cách chọn một học sinh trong nhóm là 25. Do đó, \(n\left( \Omega \right) = 25\)
Gọi A là biến cố: “Học sinh học khá môn Toán”, B là biến cố: “Học sinh học khá môn Vật lí”.
a) Khi đó, biến cố AB là: “Học sinh học khá môn Toán, đồng thời học khá môn Vật lí”
Số học sinh học khá cả 2 môn Toán và Vật lí: \(14 + 16 + 1 - 25 = 6\) nên \(n\left( {AB} \right) = 6\)
Do đó, \(P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}} = \frac{6}{{25}}\)
b) Số học sinh học khá Toán nhưng không khá Vật lí là: \(14 - 6 = 8\) (học sinh)
Xác suất để chọn được học sinh khá môn Toán, nhưng không học khá môn Vật lí là: \(\frac{8}{{25}}\)
c) Xác suất chọn được một học sinh khá môn Toán, biết rằng học sinh đó học khá môn Vật lí là: \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{\frac{6}{{25}}}}{{\frac{{16}}{{25}}}} = \frac{3}{8}\)
(Trả lời bởi datcoder)
Chuồng I có 5 con gà mái, 2 con gà trống. Chuồng II có 3 con gà mái, 5 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 3 thì bác chọn chuồng I. Nếu số chấm không chia hết cho 3 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái.
Thảo luận (1)Hướng dẫn giảiGọi A là biến cố: “Bắt được con gà mái”, B là biến cố: “Gà được bắt ở chuồng I”, \(\overline B \) là biến cố “Gà được bắt ở chuồng II”. Khi đó, \(P\left( B \right) = \frac{1}{3},P\left( {\overline B } \right) = \frac{2}{3}\).
Xác suất bắt được con gà mái nếu con gà đó ở chuồng I là: \(P\left( {A|B} \right) = \frac{5}{7}\)
Xác suất bắt được con gà mái nếu con gà đó ở chuồng II là: \(P\left( {A|\overline B } \right) = \frac{3}{8}\)
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = \frac{1}{3}.\frac{5}{7} + \frac{2}{3}.\frac{3}{8} = \frac{{41}}{{84}}\)
Vậy xác suất để bác Mai bắt được con gà mái là \(\frac{{41}}{{84}}\).
(Trả lời bởi datcoder)
Một loại vaccine được tiêm ở địa phương X. Người có bệnh nền thì với xác suất 0,35 có phản ứng phụ sau tiêm; người không có bệnh nền thì chỉ có phản ứng phụ sau tiêm với xác suất 0,16. Chọn ngẫu nhiên một người được tiêm vaccine và người này có phản ứng phụ. Tính xác suất để người này có bệnh nền, biết rằng tỉ lệ người có bệnh nền ở địa phương X là 18%.
Thảo luận (1)Hướng dẫn giảiGọi A là biến cố: “Người bị bệnh nền”, B là biến cố: “Người có phản ứng phụ sau tiêm”
Khi đó, \(P\left( A \right) = 0,18,P\left( {\overline A } \right) = 0,82\), \(P\left( {B|A} \right) = 0,35,P\left( {B|\overline A } \right) = 0,16\)
Theo công thức Bayes ta có:
\(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right)}} = \frac{{0,18.0,35}}{{0,18.0,35 + 0,82.0,16}} = \frac{{315}}{{971}}\)
Vậy xác suất để người này có bệnh nền nếu chọn ngẫu nhiên một người được tiêm vaccine biết người này có phản ứng phụ là \(\frac{{315}}{{971}}\).
(Trả lời bởi datcoder)