Cho tam giác ABC vuông tại A. Chứng minh rằng \(\frac{{AC}}{{AB}} = \frac{{\sin B}}{{\sin C}}\).
Bài tập cuối chương 4
Bài tập 11 (SGK Chân trời sáng tạo - Tập 1 - Trang 73)
Thảo luận (1)
Bài tập 12 (SGK Chân trời sáng tạo - Tập 1 - Trang 73)
Cho góc nhọn \(\alpha \) biết sin\(\alpha \) = 0,8. Tính cos\(\alpha \), tan \(\alpha \) và cot\(\alpha \).
Thảo luận (1)Hướng dẫn giảiVì sin\(\alpha \) = 0,8 nên \(\alpha \approx 53^\circ 8'\)
Suy ra \(\cos \alpha \approx \cos 53^\circ 8' \approx 0,6\)
\(\tan \alpha \approx \tan 53^\circ 8' \approx 1,3\)
\(\cot \alpha = \frac{1}{\tan \alpha} \approx 0,7\)
(Trả lời bởi datcoder)
Bài tập 13 (SGK Chân trời sáng tạo - Tập 1 - Trang 73)
Tính giá trị biểu thức:
a) \(A = 4 - {\sin ^2}{45^o} + 2{\cos ^2}{60^o} - 3{\cot ^3}{45^o}\)
b) \(B = \tan {45^o}.\cos {30^o}.\cot {30^o}\)
c) \(C = \sin {15^o} + \sin {75^o} - \cos{15^o} - \cos {75^o} + \sin {30^o}\)
Thảo luận (1)Hướng dẫn giảia) \(A = 4 - {\sin ^2}{45^o} + 2{\cos ^2}{60^o} - 3{\cot ^3}{45^o}\)
\(A= 4 - {\left( {\frac{{\sqrt 2 }}{2}} \right)^2} + 2.{\left( {\frac{1}{2}} \right)^2} - {3.1^3} = 1\)
b) \(B = \tan {45^o}.\cos {30^o}.\cot {30^o}\)
\(B = 1.\frac{{\sqrt 3 }}{2}.\sqrt 3 = \frac{3}{2}\)
c) \(C = \sin {15^o} + \sin {75^o} - \cos{15^o} - \cos {75^o} + \sin {30^o}\)
\(C = \cos {75^o} + \cos {15^o} - \cos{15^o} - \cos {75^o} + \sin {30^o}\)
\(C = \sin {30^o} = \frac{1}{2}\)
(Trả lời bởi datcoder)
Bài tập 14 (SGK Chân trời sáng tạo - Tập 1 - Trang 73)
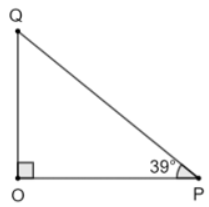
Cho tam giác OPQ vuông tại O có \(\widehat P = {39^o}\) và PQ = 10 cm. Hãy giải tam giác vuông OPQ.
Thảo luận (1)Hướng dẫn giải
Ta có \(\widehat Q = {90^o} - \widehat P = {90^o} - {39^o} = {51^o}\)
Xét tam giác PQO vuông tại O, \(\widehat Q = {51^o}\), ta có:
PQ = QP. sin \({51^o}\) = 10. sin \({51^o} \approx 7,8 cm\)
Xét tam giác PQO vuông tại O, \(\widehat P = {39^o}\), ta có:
QO = QP. sin \({39^o}\) = 10. sin\({39^o} \approx 6,3 cm\)
(Trả lời bởi datcoder)
Bài tập 15 (SGK Chân trời sáng tạo - Tập 1 - Trang 73)
Hai điểm P và Q cách nhau 203 m và thẳng hàng với chân một tòa tháp (Hình 3). Từ đỉnh của tòa tháp đó, một người nhìn thấy hai điểm P, Q với hai góc nghiêng xuống lần lượt là \({38^o}\) và \({44^o}\). Tính chiều cao của tòa tháp (kết quả làm tròn đến hàng đơn vị của mét).
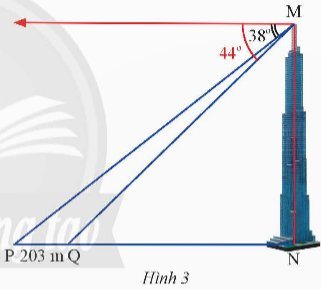
Thảo luận (1)Hướng dẫn giảiTa có: \(\widehat {QMN} = {90^o} - {44^o} = {46^o}\), \(\widehat {PMN} = {90^o} - {38^o} = {52^o}\)
Xét tam giác MQN vuông tại N, ta có:
QN = MN. tan\(\widehat {QMN}\)
Xét tam giác MPN vuông tại N, ta có:
PN = MN. tan\(\widehat {PMN}\)
Mặt khác, ta có PN – QN = 203
Suy ra MN. tan\(\widehat {PMN}\) - MN. tan\(\widehat {QMN}\) = 203
MN.( tan\(\widehat {PMN}\) - tan\(\widehat {QMN}\)) = 203
Vậy MN = \(\frac{{203}}{{\tan \widehat {PMN} - \tan \widehat {QMN}}} = \frac{{203}}{{\tan {{52}^o} - \tan {{46}^o}}} \approx 831\)
Vậy chiều cao của toàn tháp là khoảng 831 m.
(Trả lời bởi datcoder)
Bài tập 16 (SGK Chân trời sáng tạo - Tập 1 - Trang 73)
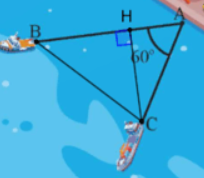
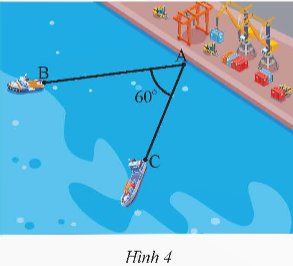
Hai điểm tàu thủy B và C cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo thành một góc 60o (Hình 4). Tàu B chạy với tốc độ 20 hải lí/giờ, tàu C chạy với tốc độ 15 hải lý/giờ. Hỏi sau 1,5 giờ hai tàu B và C cách nhau bao nhiêu hải lí (kết quả làm tròn đến hàng phần trăm)?
Thảo luận (1)Hướng dẫn giải
Xét tam giác AHC vuông tại H, có:
CH = AC. sin 60o = 22,5. sin 60o = \(\frac{45\sqrt 3}{4} \) (hải lý)
Áp dụng định lý Pythagore ta có:
AH = \(\sqrt {{{22,5}^2} - {{\left( {\frac{45\sqrt 3}{4}} \right)}^2}} = \frac{45}{4}\) (hải lý)
Suy ra \(BH = 30 – \frac{45}{4} = \frac{75}{4}\) (hải lý)
Mặt khác, tam giác CHB vuông tại H, áp dụng định lý Pythagore ta có:
BC = \(\sqrt {C{H^2} + B{H^2}} = \sqrt {{{\left( {\frac{45\sqrt 3}{4} } \right)}^2} + \left( \frac{75}{4}\right)}^2 = \frac{15\sqrt13}{2} \approx 27,04\) (hải lý)
Vậy sau 1,5 giờ hai tàu B và C cách nhau 27,04 hải lý.
(Trả lời bởi datcoder)
