Quan sát và cho biết chiếc đèn treo ở Hình 96a, trạm khảo sát trắc địa ở Hình 96b có dạng hình gì.

Quan sát và cho biết chiếc đèn treo ở Hình 96a, trạm khảo sát trắc địa ở Hình 96b có dạng hình gì.

Cho hình chóp đều \(S.ABCD\) có các cạnh bên và các cạnh đáy đều bằng \(a\).
a) Chứng minh rằng các tam giác \(ASC\) và \(BSD\) là tam giác vuông cân.
b) Gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\), chứng minh rằng đường thẳng \(SO\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\).
c) Chứng minh rằng góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^ \circ }\).
Thảo luận (1)Hướng dẫn giải
a) \(ABCD\) là hình vuông \( \Rightarrow AC = B{\rm{D}} = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Xét \(\Delta ASC\) có: \(S{A^2} + S{C^2} = 2{a^2} = A{C^2},SA = SC\)
Vậy tam giác \(ASC\) là tam giác vuông cân tại \(S\).
Xét \(\Delta BSD\) có: \(S{B^2} + S{D^2} = 2{a^2} = B{{\rm{D}}^2},SB = SD\)
Vậy tam giác \(BSD\) là tam giác vuông cân tại \(S\).
b) \(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow SO \bot AC\)
\(\Delta BSD\) vuông cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
c) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)
\(\Delta ASC\) vuông cân tại \(S\) \( \Rightarrow \widehat {SAO} = {45^ \circ }\)
Vậy \(\left( {SA,\left( {ABCD} \right)} \right) = {45^ \circ }\).
(Trả lời bởi Quoc Tran Anh Le)
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Góc giữa đường thẳng \(AC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({60^ \circ }\).
a) Chứng minh rằng hai mặt phẳng \(\left( {ACC'A'} \right)\) và \(\left( {BDD'B'} \right)\) vuông góc với nhau.
b) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(CD'\).
Thảo luận (1)Hướng dẫn giải
a) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(BB' \bot \left( {ABCD} \right) \Rightarrow BB' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {B{\rm{DD'B'}}} \right)\\AC \subset \left( {ACC'A'} \right)\end{array} \right\} \Rightarrow \left( {ACC'A'} \right) \bot \left( {B{\rm{DD}}'B'} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AB\parallel C{\rm{D}}\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C{\rm{D}}\parallel C'{\rm{D}}'\)
\( \Rightarrow AB\parallel C'{\rm{D}}' \Rightarrow d\left( {AB,C'{\rm{D}}'} \right) = d\left( {B,C'{\rm{D}}'} \right)\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow C'D' \bot B'C'\)
\(CDD'C'\) là hình chữ nhật \( \Rightarrow C'D' \bot CC'\)
\( \Rightarrow C'D' \bot \left( {BCC'B'} \right) \Rightarrow C'D' \bot BC' \Rightarrow d\left( {B,C'{\rm{D}}'} \right) = BC'\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
\(\begin{array}{l}CC' \bot \left( {ABCD} \right) \Rightarrow \left( {AC',\left( {ABCD} \right)} \right) = \left( {AC',AC} \right) = \widehat {CAC'} = {60^ \circ }\\ \Rightarrow CC' = AC.\tan \widehat {CAC'} = a\sqrt 6 \end{array}\)
\(\Delta BCC'\) vuông tại \(C \Rightarrow BC{'^2} = \sqrt {B{C^2} + CC{'^2}} = a\sqrt 7 \)
Vậy \(d\left( {AB,C'{\rm{D}}'} \right) = a\sqrt 7 \).
(Trả lời bởi Quoc Tran Anh Le)
Một chiếc bánh chưng có dạng khối hộp chữ nhật với kích thước ba cạnh là 15 cm, 15 cm và 6 cm. Tính thể tích của chiếc bánh chưng đó.
Thảo luận (2)Hướng dẫn giải
Một miếng pho mát có dạng khối lăng trụ đứng với chiều cao 10 cm và đáy là tam giác vuông cân có cạnh góc vuông bằng 12 cm. Tính khối lượng của miếng pho mát theo đơn vị gam, biết khối lượng riêng của loại pho mát đó là 3 g/cm.
Thảo luận (1)Hướng dẫn giảiDiện tích đáy của miếng pho mát là:
\(\dfrac{1}{2}.12.12=72\left(cm^2\right)\)
Thế tích miếng pho mát là:
\(72.10=720\left(cm^3\right)\)
Khối lượng miếng pho mát là:
\(3.720=2160\left(g\right)\)
(Trả lời bởi Mai Trung Hải Phong)
Một loại đèn đá muối có dạng khối chóp tứ giác đều (Hình 97). Tính theo a
thể tích của đèn đá muối đó, giả sử các cạnh đáy và các cạnh bên đều bằng a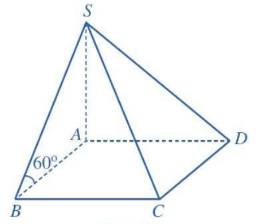
Thảo luận (1)Hướng dẫn giải
Mô hình hoá đèn đá muối bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\).
Gọi \(O\) là tâm của đáy.
\(\Delta SAC\) cân tại \(S\) \( \Rightarrow SO \bot AC\)
\(\Delta SBD\) cân tại \(S\) \( \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)
\(ABCD\) là hình vuông \( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\\{V_{S.ABC{\rm{D}}}} = \frac{1}{3}.{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\end{array}\)
(Trả lời bởi Quoc Tran Anh Le)
Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều . Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m . Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị đồng.
Thảo luận (1)Hướng dẫn giải
Mô hình hoá chân tháp bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 5,A'B' = 2,CC' = 3\).
\(ABCD\) là hình vuông
\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 5\sqrt 2 \Rightarrow CO = \frac{1}{2}AC = \frac{{5\sqrt 2 }}{2}\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow A'C' = \sqrt {A'B{'^2} + B'C{'^2}} = 2\sqrt 2 \Rightarrow C'O' = \frac{1}{2}A'C' = \sqrt 2 \)
Kẻ \(C'H \bot OC\left( {H \in OC} \right)\)
\(OHC'O'\) là hình chữ nhật \( \Rightarrow OH = O'C' = \sqrt 2 ,OO' = C'H \Rightarrow CH = OC - OH = \frac{{3\sqrt 2 }}{2}\)
\(\Delta CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{3\sqrt 2 }}{2} \Rightarrow OO' = C'H = \frac{{3\sqrt 2 }}{2}\)
Diện tích đáy lớn là: \(S = A{B^2} = {5^2} = 25\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = A'B{'^2} = {2^2} = 4\left( {{m^2}} \right)\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.\frac{{3\sqrt 2 }}{2}\left( {25 + \sqrt {25.4} + 4} \right) = \frac{{39\sqrt 2 }}{2}\left( {{m^3}} \right)\)
Số tiền để mua bê tông tươi làm chân tháp là: \(\frac{{39\sqrt 2 }}{2}.1470000 \approx 40538432\) (đồng).
(Trả lời bởi Quoc Tran Anh Le)