Trong Hình 15, cho biết a // b, Tìm số đo các góc đỉnh A và B
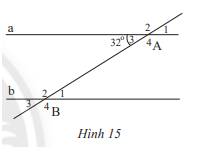
Trong Hình 15, cho biết a // b, Tìm số đo các góc đỉnh A và B

Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.
a) Vì sao cặp góc so le trong còn lại cũng bằng nhau?
b) Vì sao các cặp góc đồng vị cũng bằng nhau?
Thảo luận (1)Hướng dẫn giải
Vì đường thẳng c cắt hai đường thẳng a và b tạo thành một cặp góc so le trong ( góc A4 và B3) bằng nhau nên a // b ( Dấu hiệu nhận biết 2 đường thẳng song song)
Vì a // b nên theo tính chất của 2 đường thẳng song song:
a) Các so le trong bằng nhau
b) Các góc đồng vị bằng nhau
(Trả lời bởi Hà Quang Minh)
Hãy nói các cách để kiểm tra hai đường thẳng song song mà em biết.
Thảo luận (1)Hướng dẫn giảiCách 1: Kiểm tra 2 góc ở vị trí so le trong có bằng nhau không. Nếu bằng nhau thì 2 đường thẳng song song.
Cách 2: Kiểm tra 2 góc ở vị trí đồng vị có bằng nhau không. Nếu bằng nhau thì 2 đường thẳng song song.
Cách 3: Kiểm tra 2 đường thẳng có cùng song song với 1 đường thẳng không. Nếu có thì 2 đường thẳng song song.
Cách 4: Kiểm tra 2 đường thẳng có cùng vuông góc với 1 đường thẳng không. Nếu có thì 2 đường thẳng song song.
(Trả lời bởi Hà Quang Minh)
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
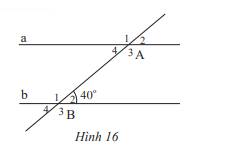
Thảo luận (1)Hướng dẫn giảia) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
(Trả lời bởi Hà Quang Minh)
Cho Hình 17, biết a // b.
Tính số đo các góc \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\)
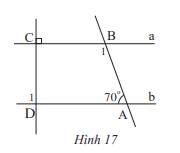
Thảo luận (1)Hướng dẫn giải
Cách 1: Vì a//b, a \( \bot \) CD nên b \( \bot \) CD. Do đó, \(\widehat {{D_1}}=90^\circ \).
Vì a//b nên \(\widehat {{A_1}} + \widehat {{B_1}}=180^0\) (2 góc trong cùng phía) nên \(\widehat {{B_1}} + 70^\circ = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 70^\circ = 110^\circ \)
Vậy \(\widehat {{B_1}} =110^0; \widehat {{D_1}}=90^\circ \).
Cách 2: Vì a // b nên
+) \(\widehat {{C_1}} = \widehat {{D_2}}\) ( 2 góc đồng vị), mà \(\widehat {{C_1}} = 90^\circ \) nên \(\widehat {{D_2}} = 90^\circ \). Do đó, b\( \bot \) CD nên \(\widehat {{D_1}}=90^\circ \)
+) \(\widehat {{A_1}} = \widehat {{B_2}}\) ( 2 góc so le trong) nên \(\widehat {{B_2}} = 70^\circ \)
Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \)( 2 góc kề bù) nên \(\widehat {{B_1}} + 70^\circ = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 70^\circ = 110^\circ \).
Vậy \(\widehat {{B_1}} =110^0; \widehat {{D_1}}=90^\circ \).
(Trả lời bởi Hà Quang Minh)
Cho Hình 18, biết \(\widehat {{B_1}} = 40^\circ ,\widehat {{C_2}} = 40^\circ \)
a) Đường thẳng a có song song với đường thẳng b không? Vì sao?
b) Đường thẳng b có song song với đường thẳng c không? Vì sao?
c) Đường thẳng a có song song với đường thẳng c không? Vì sao?
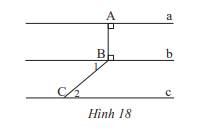
Thảo luận (1)Hướng dẫn giảia) Vì a,b cùng vuông góc với đường thẳng AB nên a // b
b) Vì \(\widehat {{B_1}} = \widehat {{C_2}}( = 40^\circ )\). Mà 2 góc này ở vị trí so le trong nên b // c ( Dấu hiệu nhận biết 2 đường thẳng song song)
c) Vì a // b, b //c nên a // c
(Trả lời bởi Hà Quang Minh)
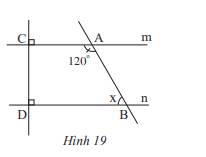
Quan sát Hình 19 và cho biết:
a) Vì sao m // n?
b) Số đo x của góc \(\widehat {ABD}\) là bao nhiêu?
Thảo luận (1)Hướng dẫn giải
a) Vì m và n cùng vuông góc với CD nên m // n
b) Ta có: \(\widehat {{A_2}} + \widehat {{A_1}} = 180^\circ \Rightarrow 120^\circ + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - 120^\circ = 60^\circ \)
Vì m // n nên \(\widehat {{A_1}} = \widehat {ABD}\) ( 2 góc so le trong) nên \(\widehat {ABD}\) = 60\(^\circ \)
Vậy x = 60\(^\circ \)
(Trả lời bởi Hà Quang Minh)