Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân.
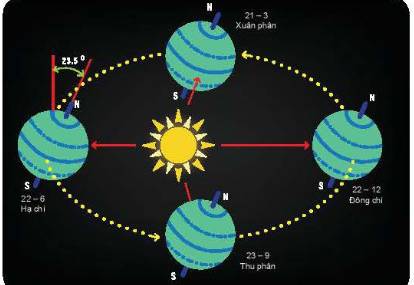
a) Dưới ánh sáng mặt trời, bóng của cây cột trên sân có thể được nhìn như là hình chiếu của cây cột qua phép chiếu song song hay không?
b) Khi tia sáng mặt trời vuông góc với mặt sân, liệu ta có thể quan sát được bóng của cây cột trên sân hay không?