Cho (H): \(\frac{{{x^2}}}{{144}} - \frac{{{y^2}}}{{25}} = 1\). Tìm các tiêu điểm và tiêu cự của (H).
Bài 22: Ba đường conic
Luyện tập 4 (SGK Kết nối tri thức với cuộc sống trang 50-52)
Thảo luận (1)
Hoạt động 5 (SGK Kết nối tri thức với cuộc sống trang 52,53)
Cho parabol (P): \(y = \frac{1}{4}{x^2}\). Xét F(0; 1) và đường thẳng\(\Delta :{\rm{ }}y{\rm{ }} + 1 = 0\) . Với điểm M(x;y) bất kì, chứng minh rằng \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \) M(xy) thuộc (P).
Thảo luận (1)Hướng dẫn giảiTa có: \(MF = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} ,d\left( {M,\Delta } \right) = \left| {y + 1} \right|\).
Xét \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \left| {y + 1} \right| \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2} \Leftrightarrow {x^2} = 4y \Leftrightarrow y = \frac{1}{4}{x^2}\).
Vậy tập hợp điểm M để \(MF{\rm{ }} = \;d\left( {M,\Delta } \right)\) là parabol \(y = \frac{1}{4}{x^2}\)
(Trả lời bởi Hà Quang Minh)
Hoạt động 6 (SGK Kết nối tri thức với cuộc sống trang 52-53)
Xét (P) là một parabol với tiêu điểm F và đường chuẩn Delta . Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên Delta . Chọn hệ trục toạ độ Oxy Có gốc O là trung điểm của HF, tia Ox trùng tia OF (H7.27).a) Nêu toạ độ của Fvà phương trình của Delta .b) Giải thích vì sao điềm M(x; y) thuộc (P) khi và chỉ khi sqrt {{{left( {x - frac{p}{2}} right)}^2} + {y^2}} left| {x + frac{p}{2}} right|.
Đọc tiếp
Xét (P) là một parabol với tiêu điểm F và đường chuẩn \(\Delta \). Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên \(\Delta \). Chọn hệ trục toạ độ Oxy Có gốc O là trung điểm của HF, tia Ox trùng tia OF (H7.27).
a) Nêu toạ độ của Fvà phương trình của \(\Delta \).
b) Giải thích vì sao điềm M(x; y) thuộc (P) khi và chỉ khi \(\sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Thảo luận (1)Hướng dẫn giảia) Tọa độ điểm F là: \(F\left( {\frac{p}{2};0} \right)\) và phương trình đường chuẩn là: \(\Delta :x = - \frac{p}{2}\)
b) Ta có: \(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} ,d\left( {M,\Delta } \right) = \left| {x + \frac{p}{2}} \right|\). Để M thuộc (P) thì \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 2 (SGK Kết nối tri thức với cuộc sống trang 52,53)
Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gi? Vì sao?
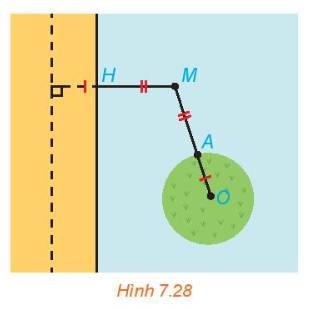
Thảo luận (1)Hướng dẫn giảiGọi d là đường thẳng nằm trong đất liền, song song với bờ biển và cách bờ biển một khoảng bằng bán kính OA.
Ta có: \(d\left( {M,d} \right) = MH + R = MA + AO = MO\)
Vậy tập hợp điểm M thuộc (P) có tiêu điểm là O. Đường chuẩn là d. Do đó đường ranh giới cần tìm là đường parabol (P).
(Trả lời bởi Hà Quang Minh)
Vận dụng 3 (SGK Kết nối tri thức với cuộc sống trang 54-56)
Gương elip trong một máy tán sỏi thận (H7.33) ứng với clip có phương trình chính tắc là \(\frac{{{x^2}}}{{400}} + \frac{{{y^2}}}{{76}} = 1\) (theo đơn vị cm). Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.

Thảo luận (1)Hướng dẫn giảiVị tri bắt đầu phát sóng của máy và vị trí viên sỏi được đặt ở hai tiêu điểm của gương elip, do đó khoảng cách cần tìm là tiêu cự của gương và bằng \(2c = 2\sqrt {400 - 76} = 36\left( {cm} \right)\).
(Trả lời bởi Hà Quang Minh)
Bài 7.19 (SGK Kết nối tri thức với cuộc sống trang 56)
Cho Elip có phương trình \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của elip.
Thảo luận (1)Hướng dẫn giảiTa có: \({a^2} = 36,{b^2} = 9 \Rightarrow c = \sqrt {36 - 9} = 3\sqrt 3 \) nên elip có hai tiêu điểm là \({F_1}\left( { - 3\sqrt 3 ;0} \right);{F_2}\left( {3\sqrt 3 ;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\sqrt 3 \).
(Trả lời bởi Hà Quang Minh)
Bài 7.20 (SGK Kết nối tri thức với cuộc sống trang 56)
Cho hyperbol có phương trình \(\frac{{{x^2}}}{7} - \frac{{{y^2}}}{9} = 1\). Tìm tiêu điểm và tiêu cự của hyperbol.
Thảo luận (1)Hướng dẫn giảiTa có: \({a^2} = 7,{b^2} = 9 \Rightarrow c = \sqrt {7 + 9} = 4\) nên hypebol có hai tiêu điểm là \({F_1}\left( { - 4;0} \right);{F_2}\left( {4;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 8\).
(Trả lời bởi Hà Quang Minh)
Bài 7.21 (SGK Kết nối tri thức với cuộc sống trang 56)
Cho parabol có phương trình \({y^2} = 8x\). Tìm tiêu điểm và đường chuẩn của parabol.
Thảo luận (1)Hướng dẫn giảiTa có: \(2p = 8 \Rightarrow p = 4\) nên (P) có tiêu điểm là \(F\left( {2;0} \right)\) và đường chuẩn là \(x = - 2\).
(Trả lời bởi Hà Quang Minh)
Bài 7.22 (SGK Kết nối tri thức với cuộc sống trang 56)
Lập phương trình chính tắc của elip đi qua hai điểm \(A\left( {5;0} \right)\) và có một tiêu điểm là \({F_2}\left( {3;0} \right)\).
Thảo luận (1)Hướng dẫn giảiPhương trình chính tắc của elip có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\).
Elip đi qua \(A\left( {5;0} \right)\) nên ta có \(\frac{{{5^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Leftrightarrow {a^2} = 25\)
Mặt khác elip có một tiêu điểm \({F_2} = \left( {3;0} \right)\) nên ta có \(c = 3\), suy ra \({b^2} = {a^2} - {c^2} = 25 - {3^2} = 16\)
Vậy phương trình của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
(Trả lời bởi Hà Quang Minh)
Bài 7.23 (SGK Kết nối tri thức với cuộc sống trang 56)
Lập phương trình chính tắc của parabol đi qua điểm \(M\left( {2;4} \right)\).
Thảo luận (1)Hướng dẫn giảiPhương trình chính tắc của (P) có dạng \({y^2} = 2px\left( {p > 0} \right)\)
Vì (P) đi qua điểm \(M\left( {2;4} \right)\) nên ta có \({4^2} = 2p.2 \Leftrightarrow p = 4\).
Vậy phương trình chính tắc của (P) là \({y^2} = 8x\).
(Trả lời bởi Hà Quang Minh)