Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Bài 2: Hàm số bậc hai
Bài 3 (SGK Chân trời sáng tạo trang 56)
Thảo luận (1)
Bài 4 (SGK Chân trời sáng tạo trang 56)
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Thảo luận (1)Hướng dẫn giảiTham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
(Trả lời bởi Kiều Sơn Tùng)
Bài 5 (SGK Chân trời sáng tạo trang 56)
Cho hàm số \(y = 2{x^2} + x + m\). Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.
Thảo luận (1)Hướng dẫn giảiTham khảo:
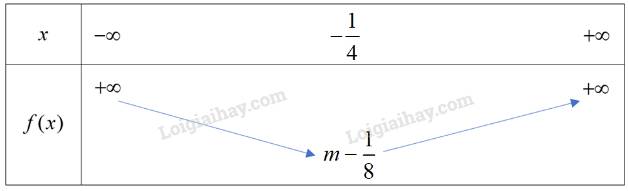
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 1}}{{2.2}} = - \frac{1}{4};{y_S} = f( - \frac{1}{4}) = 2{\left( { - \frac{1}{4}} \right)^2} + \left( { - \frac{1}{4}} \right) + m = m - \frac{1}{8}\)
Ta có: \(a = 2 > 0\), hàm số có bảng biến thiên dạng:
Hàm số đạt giá trị nhỏ nhất bằng \(m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{{41}}{8}.\)
Vậy \(m = \frac{{41}}{8}\) thì hàm số đạt giá trị nhỏ nhất bằng 5.
(Trả lời bởi Kiều Sơn Tùng)
Bài 6 (SGK Chân trời sáng tạo trang 56)
Vẽ đồ thị các hàm số sau:
a) \(y = 2{x^2} + 4x - 1\)
b) \(y = - {x^2} + 2x + 3\)
c) \(y = - 3{x^2} + 6x\)
d) \(y = 2{x^2} - 5\)
Thảo luận (1)Hướng dẫn giảiTham khảo:
a)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} + 4x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
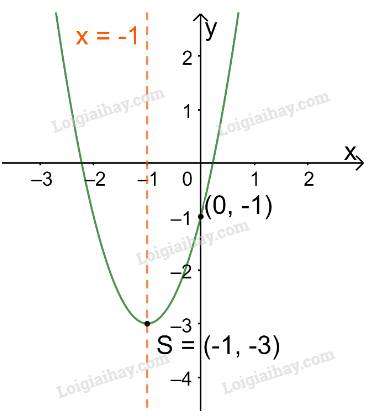
b)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
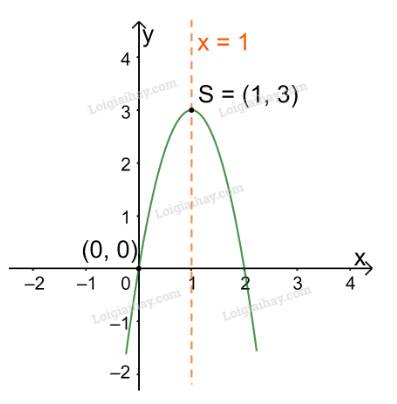
c)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - 3{x^2} + 6x\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 3 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).
Ta vẽ được đồ thị như hình dưới.
d)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} - 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.\)
+ Có trục đối xứng là đường thẳng \(x = 0\) (trùng với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).
Ta vẽ được đồ thị như hình dưới.
(Trả lời bởi Kiều Sơn Tùng)
Bài 7 (SGK Chân trời sáng tạo trang 56)
Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.
\(\begin{array}{l}({P_1}):y = - 2{x^2} - 4x + 2;\\({P_2}):y = 3{x^2} - 6x + 5;\\({P_3}):y = 4{x^2} - 8x + 7;\\({P_4}):y = - 3{x^2} - 6x - 1.\end{array}\)

Thảo luận (1)Hướng dẫn giảiVì 4 đồ thị hàm số cắt trục tung tại 4 điểm phân biệt nên ta chỉ cần xác định tọa độ giao điểm của mỗi hàm số với trục tung là có thể phân biệt 4 đồ thị hàm số.
Đồ thị hàm số \(({P_1}):y = - 2{x^2} - 4x + 2\) cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2) => Đồ thị là đường màu xanh lá.
Đồ thị hàm số \(({P_2}):y = 3{x^2} - 6x + 5;\) cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5) => Đồ thị là đường màu xanh dương.
Đồ thị hàm số \(({P_3}):y = 4{x^2} - 8x + 7;\) cắt trục tung tại điểm có tung độ bằng 7, tức là đồ thị đi qua điểm có tọa độ (0; 7) => Đồ thị là đường màu nâu đỏ.
Đồ thị hàm số \(({P_4}):y = - 3{x^2} - 6x - 1\) cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1) => Đồ thị là đường màu vàng.
(Trả lời bởi Hà Quang Minh)
Bài 8 (SGK Chân trời sáng tạo trang 57)
Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.
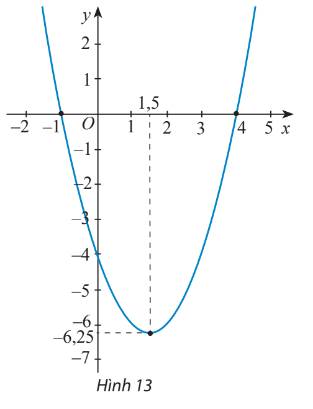
Thảo luận (1)Hướng dẫn giảiGọi công thức của hàm số bậc hai là \(y = a{x^2} + bx + c\)
Đồ thị hàm số đi qua 3 điểm có tọa độ (-1;0), (4;0), (0;-4)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a.{( - 1)^2} + b.( - 1) + c = 0\\a{.4^2} + b.4 + c = 0\\a{.0^2} + b.0 + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b + c = 0\\16a + 4b + c = 0\\c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a - b = 4\\16a + 4b = 4\\c = - 4\end{array} \right.\\ \Leftrightarrow a = 1,b = - 3,c = - 4.\end{array}\)
Vậy hàm số cần tìm có công thức \(y = {x^2} - 3x - 4\)
(Trả lời bởi Hà Quang Minh)
Bài 9 (SGK Chân trời sáng tạo trang 57)
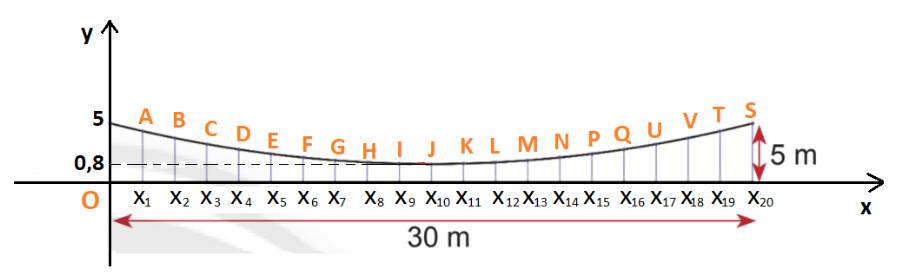
Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:- Dây dài nhất là 5 m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.- Nhịp cầu dài 30 m.- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.
Đọc tiếp
Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.
Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:
- Dây dài nhất là 5 m, dây ngắn nhất là 0,8 m. Khoảng cách giữa các dây bằng nhau.
- Nhịp cầu dài 30 m.
- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Thảo luận (1)Hướng dẫn giảiGọi \(y = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là thành cầu.
Chọn hệ trục tọa độ Oxy như hình dưới:
Khi đó độ dài dây cáp dọc ở mỗi mặt bên là tung độ của điểm biểu diễn tương ứng.
Ở mỗi mặt: có 21 dây cáp dọc, tương ứng cho 20 khoảng cách giữa chúng.
Khoảng cách giữa hai dây cáp liền kề là: \(30:20 = 1,5\left( m \right)\)
Khi đó: \({x_0} = 0;{x_1} = 1,5;\;{x_2} = 3;\;{x_3} = 4,5;\;...;{x_n} = 1,5.n\;\)
Dễ thấy: các điểm có tọa độ (0; 5), (\({x_{10}};0,8\)), \(({x_{20}};5)\) thuộc đồ thị hàm số.
(Trong đó: \({x_{10}} = 10.1,5 = 15;\;{x_{20}} = 20.1,5 = 30.\))
Suy ra:
\(f(0) = a{.0^2} + b.0 + c = 5 \Leftrightarrow c = 5\)
Và \(f(1) = a{.15^2} + b.15 + c = 0,8 \Leftrightarrow 225a + 15b + 5 = 0,8\)
\(f(2) = a{.30^2} + b.30 + c = 5 \Leftrightarrow 900a + 30b + 5 = 5\)
Giải hệ phương trình \(\left\{ \begin{array}{l}225a + 15b + 5 = 0,8\\900a + 30b + 5 = 5\end{array} \right.\) ta được \(a = \frac{{7}}{{375}};b = - \frac{{14}}{{25}}\)
Như vậy \(y = \frac{{7}}{{375}}{x^2} - \frac{{14}}{{25}}x + 5\)
Gọi \({y_0},{y_1},{y_2},..{y_{20}}\) là tung độ của các điểm có hoành độ lần lượt là \({x_0},{x_1},{x_2},..{x_{20}}\)
Ta có:
\(\begin{array}{l}{y_0} = 5\\{y_1} = \frac{{7}}{{375}}.1,{5^2} - \frac{{14}}{{25}}.1,5 + 5\\{y_2} = \frac{{7}}{{375}}.{(2.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {2^2}.\frac{{7}}{{375}}.1,{5^2} - 2.\frac{{14}}{{25}}.1,5 + 5\\...\\{y_n} = \frac{{7}}{{375}}.{(n.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {n^2}.\frac{{7}}{{375}}.1,{5^2} - n.\frac{{14}}{{25}}.1,5 + 5\\ \Rightarrow T = {y_0} + {y_1} + {y_2} + .. + {y_{20}} = 5 + \frac{{7}}{{375}}.1,{5^2}.(1 + {2^2} + ... + {20^2}) - \frac{{14}}{{25}}.1,5.(1 + 2 + ... + 20) + 5.20\end{array}\)
Mà \(1 + {2^2} + ... + {20^2} = 2870;\;1 + 2 + ... + 20 = 210\)
\( \Rightarrow T = 5 + \frac{{7}}{{375}}.1,{5^2}.2870 - \frac{{14}}{{25}}.1,5.210 + 5.20 \approx 49,14(m)\)
Do cần tính thêm 5% chiều dài để neo cố định và cần 2 thành mặt cầu nên tổng chiều dài của các dây cáp cần sử dụng là: \(49,14.2.105% = 103,2(m)\)
Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên là 103,2m.
(Trả lời bởi Hà Quang Minh)