Bài 18. Hàm số y = ax² (a ≠ 0)

Hướng dẫn giải

a) Thay lần lượt các giá trị x = –3; x = –2; …; x = 3 vào hàm số y = 2x², ta được bảng giá trị:

x	–3	–2	–1	0	1	2	3
y = 2x2	18	8	2	0	2	8	18

b) Biểu diễn các điểm \(\left( { - 3;18} \right);\left( { - 2;8} \right);\left( { - 1;2} \right);\left( {0;0} \right);\left( {3;18} \right);\left( {2;8} \right);\left( {1;2} \right)\) trên mặt phẳng tọa độ Oxy ta được:

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

a) Thể tích của hình chóp là: 

\(V = \frac{1}{3}S.h = \frac{1}{3}a^2.15 = 5a^2 (cm^3)\).

Với a = 5cm, ta có:

\(V = 5.5^2 = 135 (cm^3)\)

b) Sau khi độ dài cạnh đáy tăng lên hai lần thì độ dài cạnh đáy mới là a' = 2a (cm).

Khi đó thể tích của hình chóp là:

\(V' = 5a'^2 = 5.(2a)^2=20a^2 = 4V\).

Vậy khi độ dài cạnh đáy tăng lên hai lần thì thể tích của hình chóp tăng lên 4 lần.

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

Thay lần lượt các giá trị $x=-3 ; x=-2 ; \ldots ; x=3$ vào hàm số $y=-\frac{3}{2} x^2$. ta được bảng giá trị:

x	-3	-2	-1	0	1	2	3
\(y=-\dfrac{3}{2}x^2\)	\(-\dfrac{27}{2}\)	-6	\(-\dfrac{3}{2}\)	0	\(-\dfrac{3}{2}\)	-6	\(-\dfrac{27}{2}\)

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

a) Công thức diện tích S của hình tròn bán kính r là: \(S = \pi {r^2}\).

b) Hoàn thành bảng:

r (cm)	1	2	3	4
S (cm2)	3,14	12,56	28,26	50,24

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

a) Thay t = 0 vào công thức s = 4,9t², ta được: s = 4,9 . 02 = 0.

Thay t = 1 vào công thức s = 4,9t², ta được: s = 4,9 . 12 = 4,9.

Thay t = 2 vào công thức s = 4,9t², ta được: s = 4,9 . 22 = 19,6.

Ta hoàn thành được bảng như sau:

t (giây)	0	1	2
s (m)	0	4,9	19,6

b) Vật rơi tự do từ độ cao 19,6 mét so với mặt đất tức là quãng đường chuyển động của vật là s = 19,6 (m).

Từ bảng kết quả câu a, ta thấy khi t = 2 (giây) thì s = 19,6 (mét).

Vậy nếu một vật rơi tự do từ độ cao 19,6 m so với mặt đất thì sau 2 giây vật sẽ chạm đất.

(Trả lời bởi Nguyễn Quốc Đạt)

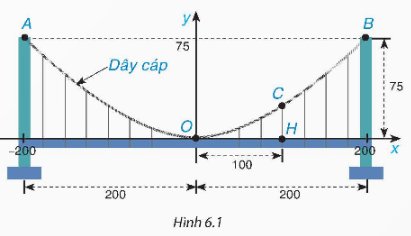
Hướng dẫn giải

Vì các dây cáp có dạng đồ thị của hàm số y = ax² (a ≠ 0) được treo trên các đỉnh tháp nên đồ thị hàm số y = ax² (a ≠ 0) đi qua điểm B(200; 75).

Thay x = 200 và y = 75 vào hàm số y = ax², ta được:

75 = a . 2002, hay 40 000a = 75, suy ra a = 0,001875 (thỏa mãn a ≠ 0).

Khi đó ta có hàm số y = 0,001875x².

Chiều cao CH của dây cáp chính là tung độ của điểm C thuộc đồ thị hàm số y = 0,001875x².

Thay hoành độ điểm C là x = 100 vào hàm số y = 0,001875x², ta được:

y = 0,001875 . 100² = 18,75.

Vậy chiều cao CH của dây cáp là 18,75 mét.

(Trả lời bởi Nguyễn Quốc Đạt)