Question

Một cổng vòm được thiết kế dạng parabol y = ax² như Hình 6.8. Biết chiều rộng của chân cổng là AB = 6 m và chiều cao của cổng là OI = 4,5 m.

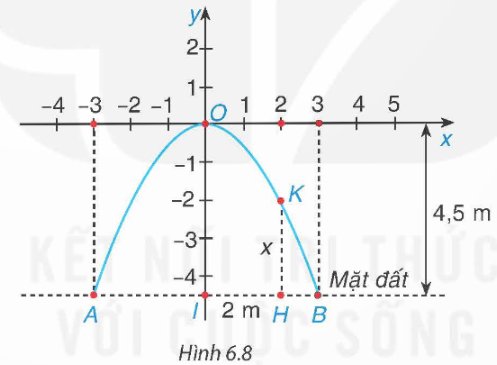
a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2 m.

b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2 m, chiều cao 3 m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?

Answer 1

a)

Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(\left( {3; - \frac{9}{2}} \right)\) nên ta có:

\( - \frac{9}{2} = a{.3^2} \Rightarrow a =  - \frac{1}{2}\).

Khi đó, \(y =  - \frac{1}{2}{x^2}\).

Ta có: \(H(2;-4,5)\); \(K(2;y_K)\)

Vì K thuộc đồ thị hàm số \(y =  - \frac{1}{2}{x^2}\) nên \(y_K = -\frac{1}{2}{2^2}= -2\) nên \(K(2;-2)\)

Từ đó ta có: \(HK = 4,5 - 2 = 2,5\left( m \right)\).

b) Cổng vòm có chiều cao bằng \(OI = 4,5m\) và chiều rộng \(AB = 6m\).

Với \(x = 1\) thì \(y =  - \frac{1}{2}{.1^2} =  - \frac{1}{2}\).

Vì \(4,5 - \left| { - \frac{1}{2}} \right| > 3\) nên xe tải này có thể đi qua cổng vòm được.