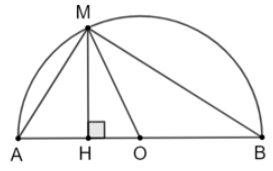
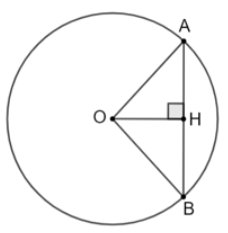
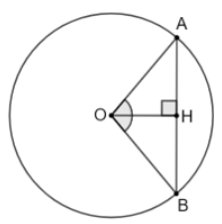
Trong các cuộc thi đấu thể thao, người ta thường tổ chức thi bắn cung. Thuở xưa, cây cung được làm ra bằng cách buộc một sợi dây (gọi là dây cung) vào hai đầu của một đoạn tre (hoặc gỗ) có tính đàn hồi cao. Đoạn tre bị kéo căng, cong lại tạo nên hình ảnh của một phần đường tròn, đó cũng chính là hình ảnh “cung” trong Toán học. Trong bài này chúng ta sẽ tìm hiểu về những vấn đề liên quan đến khái niệm này.