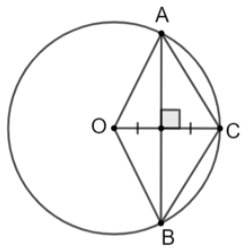
AB là đường trung trực của AB của OC nên AC = OA (tính chất đường trung trực)
mà OA = OC = R nên AC = OA = OC
hay \(\Delta \,ACO\) là tam giác đều.
Do đó: \(\widehat{AOC}=60{}^\circ \) (tính chất của tam giác đều) \(\Rightarrow \) sđ \(\overset\frown{AC}=60{}^\circ \)
Tương tự ta có: sđ \(\overset\frown{BC}=60{}^\circ \)
Suy ra:
sđ \(\overset\frown{ACB}=\)sđ \(\overset\frown{AC}\) + sđ \(\overset\frown{BC}=60{}^\circ +60{}^\circ =120{}^\circ \)
\(\overset\frown{ABC}\) là cung lớn có chung hai mút A, C với cung nhỏ \(\overset\frown{AC}\)
nên sđ \(\overset\frown{ABC}=360{}^\circ -\) sđ\(\overset\frown{AC}=360{}^\circ -60{}^\circ =300{}^\circ \)