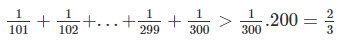Tính tích \(P=\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right).....\left(1-\dfrac{1}{99}\right)\)
Bài 11: Tính chất cơ bản của phép nhân phân số
Bài 11.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Thảo luận (1)
Bài 11.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Chứng tỏ rằng :
\(\dfrac{1}{101}+\dfrac{1}{102}+.....+\dfrac{1}{299}+\dfrac{1}{300}>\dfrac{2}{3}\)
Thảo luận (2)Hướng dẫn giải
Bài 11.5* - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Tính tích \(A=\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}....\dfrac{899}{900}\)
Thảo luận (1)Hướng dẫn giải\(A=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot...\cdot\dfrac{899}{900}\\ =\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot\dfrac{3\cdot5}{4\cdot4}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\\ =\dfrac{1\cdot2\cdot3\cdot...\cdot29}{2\cdot3\cdot4\cdot...\cdot30}\cdot\dfrac{3\cdot4\cdot5\cdot...\cdot31}{2\cdot3\cdot4\cdot...\cdot30}\\ =\dfrac{1}{30}\cdot\dfrac{31}{2}\\ =\dfrac{31}{60}\)
Vậy ...
(Trả lời bởi Lê Thị Hồng Vân)
Bài 11.6* - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Chứng tỏ rằng :
\(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+....+\dfrac{1}{17}< 2\)
Thảo luận (3)Hướng dẫn giảiTa có :\(\dfrac{1}{5}< \dfrac{1}{4};\dfrac{1}{6}< \dfrac{1}{4};\dfrac{1}{7}< \dfrac{1}{4};\dfrac{1}{8}< \dfrac{1}{4}\)
\(\Rightarrow\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{8}< \dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{4}{4}=1\left(1\right)\)
Ta có :\(\dfrac{1}{9}< \dfrac{1}{8};\dfrac{1}{10}< \dfrac{1}{8};\dfrac{1}{11}< \dfrac{1}{8};...;\dfrac{1}{17}< \dfrac{1}{8}\)
\(\Rightarrow\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{17}< \dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}+...+\dfrac{1}{8}=\dfrac{8}{8}=1\left(2\right)\)
Từ (1) và (2)\(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 1+1=2\)
Vậy \(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 2\)
(Trả lời bởi Vũ Văn Thành)
Bài 11.7* - Bài tập bổ sung (Sách bài tập - tập 2 - trang 28)
Tính giá trị của biểu thức :
\(M=\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+....+\dfrac{1}{10.11.12}\)
Thảo luận (2)Hướng dẫn giảiTa có :
\(\dfrac{1}{1.2}-\dfrac{1}{2.3}=\dfrac{3}{1.2.3}-\dfrac{1}{1.2.3}=\dfrac{2}{1.2.3}\)
\(\dfrac{1}{2.3}-\dfrac{1}{3.4}=\dfrac{4}{2.3.4}-\dfrac{2}{2.3.4}=\dfrac{2}{2.3.4}\)
...
Do đó :
\(\dfrac{1}{1.2.3}=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}\right)\)
\(\dfrac{1}{2.3.4}=\dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}\right)\)
Vậy :
\(M=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{2.3}+\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}+...+\dfrac{1}{10.11}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{1.2}-\dfrac{1}{11.12}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{132}\right)\)
\(=\dfrac{1}{2}.\dfrac{65}{132}=\dfrac{65}{264}\)
(Trả lời bởi Komorebi)