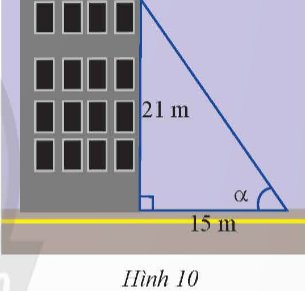
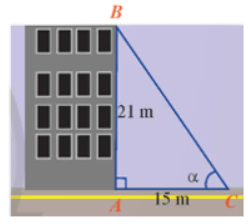
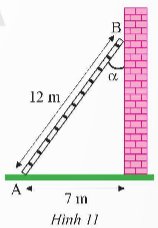
a) Vẽ một tam giác vuông có góc bằng 40o . Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40o . Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.
b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thức đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.