Số liệu về lượng mưa M (mm) trong 7 tháng mùa mưa của thành phố Đà Lạt năm 2020 được biểu diễn theo số n chỉ số trong tháng có biểu đồ dưới đây.
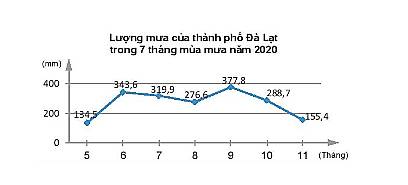
Quan sát biểu đồ và cho biết lượng mưa ở mỗi tháng là bao nhiêu?
Số liệu về lượng mưa M (mm) trong 7 tháng mùa mưa của thành phố Đà Lạt năm 2020 được biểu diễn theo số n chỉ số trong tháng có biểu đồ dưới đây.

Quan sát biểu đồ và cho biết lượng mưa ở mỗi tháng là bao nhiêu?
a) Nhiệt độ cơ thể d \(\left( {^\circ C} \right)\) của bệnh nhân theo thời gian h (giờ) trong ngày được ghi trong bảng sau:

Ứng với mỗi giờ em đọc được bao nhiêu số chỉ nhiệt độ?
b) Thời gian \(t\) (giờ) để một vật chuyển động đều đi hết quãng đường 180 km tỉ lệ nghịch với vận tốc \(v\) (km/h) của nó theo công thức \(t = \dfrac{{180}}{v}\).
Tính và lập bảng các giá trị tương ứng của \(t\) và \(v\) lần lượt bằng 10; 20; 30; 60; 180.
Ứng với mỗi giá trị của đại lượng \(v\) em tính được bao nhiêu giá trị của đại lượng \(t\)?
Thảo luận (1)Hướng dẫn giảia) Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ.
Ứng với 7h thì nhiệt độ là \(36^\circ C\)
Ứng với 8h thì nhiệt độ là \(37^\circ C\)
Ứng với 9h thì nhiệt độ là \(36^\circ C\)
Ứng với 10h thì nhiệt độ là \(37^\circ C\)
Ứng với 11h thì nhiệt độ là \(38^\circ C\)
Ứng với 12h thì nhiệt độ là \(37^\circ C\)
Ứng với 13h thì nhiệt độ là \(38^\circ C\)
Ứng với 14h thì nhiệt độ là \(39^\circ C\)
Ứng với 15h thì nhiệt độ là \(39^\circ C\)
b) Với \(v = 10 \Rightarrow t = \dfrac{{180}}{{10}} = 18\)
Với \(v = 20 \Rightarrow t = \dfrac{{180}}{{20}} = 9\)
Với \(v = 30 \Rightarrow t = \dfrac{{180}}{{30}} = 6\)
Với \(v = 60 \Rightarrow t = \dfrac{{180}}{{60}} = 3\)
Với \(v = 180 \Rightarrow t = \dfrac{{180}}{{180}} = 1\)
Lập bảng:
(Trả lời bởi Hà Quang Minh)
\(v\)
10
20
30
60
180
\(t\)
18
9
6
3
1
Mô tả các đại lượng là hàm số và biến số trong các mô hình sau:
a) Biểu đồ cột chỉ doanh thu \(y\) (triệu đồng) của một cửa hàng trong các tháng \(x\).
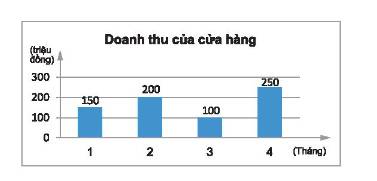
b) Quãng đường \(s\) (km) đi được trong khoảng thời gian \(t\) (giờ) của một chiếc xe chạy với tốc độ không đổi bằng 40 km/h.
c) Số tiền \(y\) (đồng) người mua phải trả cho \(x\) quyển vở có giá trị 10 000 đồng/ quyển.
Thảo luận (1)Hướng dẫn giảia) Đại lượng là hàm số là doanh thu (triệu đồng) của một cửa hàng và biến số là tháng x.
b) Đại lượng là hàm số là quãng đường đi được và biến số là thời gian .
c) Đại lượng là hàm số là số tiền người mua phải trả và biến số là số quyển vở.
(Trả lời bởi Hà Quang Minh)
Khi đo nhiệt độ, ta có công thức đổi từ đơn vị độ C (Celsius) sang đơn vị độ F (Fahrenheit) như sau: F = 1,8C + 3,2. Theo em, F có phải làm một hàm số theo biến số C hay không? Giải thích.
Thảo luận (1)Hướng dẫn giảiF là một hàm số theo biến C vì với mỗi giá trị của C chỉ cho ta duy nhất một giá trị của F.
(Trả lời bởi Hà Quang Minh)
Cho biết đại lượng \(y\) được tính theo đại lượng \(x\) như sau: \(y = 2x + 3\)

a) Tính \(y\) khi \(x = 4\).
b) Cho \(x\) một giá trị tùy ý, tính giá trị tương ứng của \(y\).
Thảo luận (1)Hướng dẫn giảiVới \(x = 4\) ta được. \(y = 2.4 + 3 = 11\)
Với \(x = 6\) ta được. \(y = 2.6 + 3 = 15\)
(Trả lời bởi Hà Quang Minh)
\(x\)
1
2
3
4
6
\(y = 2x + 3\)
5
7
9
11
15
a) Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau:

Đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không?
b) Cho hàm số \(y = f\left( x \right) = {x^2}\)
- Tính \(f\left( 2 \right);f\left( { - 3} \right)\).
- Lập bảng giá trị của hàm số với \(x\) lần lượt bằng \( - 3; - 2; - 1;0;1;2;3\).
Thảo luận (1)Hướng dẫn giảia) Đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ xác nhận được duy nhất một giá trị \(y\) tương ứng.
b) \(f\left( 2 \right) = {2^2} = 4;f\left( { - 3} \right) = {\left( { - 3} \right)^2} = 9\)
Ta có: \(f\left( { - 2} \right) = {\left( { - 2} \right)^2} = 4;f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\(f\left( 0 \right) = {0^2} = 0;f\left( 1 \right) = {1^2} = 1\)
\(f\left( 2 \right) = {2^2} = 4;f\left( 3 \right) = {3^2} = 9\)
(Trả lời bởi Hà Quang Minh)
\(x\)
–3
–2
–1
0
1
2
3
\(f\left( x \right)\)
9
4
1
0
1
4
9
Cho \(C = f\left( d \right)\)là hàm số mô tả mối quan hệ giữa chu vi \(C\) và đường kính \(d\) của một đường tròn. Tìm công thức \(f\left( d \right)\) và lập bảng giá trị của hàm số ứng với \(d\) lần lượt bằng \(1;2;3;4\) (theo đơn vị cm).
Thảo luận (1)Hướng dẫn giảiTa có: \(C = \pi .d\) trong đó, \(C\) là chu vi đường tròn; \(d\) là đường kính và \(\pi \) là số pi.
Do đó, \(f\left( d \right) = \pi .d\)
Với \(d = 1 \Rightarrow f\left( 1 \right) = \pi .1 = \pi \);
\(d = 2 \Rightarrow f\left( 2 \right) = \pi .2 = 2\pi \);
\(d = 3 \Rightarrow f\left( 3 \right) = \pi .3 = 3\pi \);
\(d = 4 \Rightarrow f\left( 4 \right) = \pi .4 = 4\pi \).
Ta thu được bảng sau:
(Trả lời bởi Hà Quang Minh)
\(d\)
1
2
3
4
\(f\left( d \right)\)
\(\pi \)
\(2\pi \)
\(3\pi \)
\(4\pi \)
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.
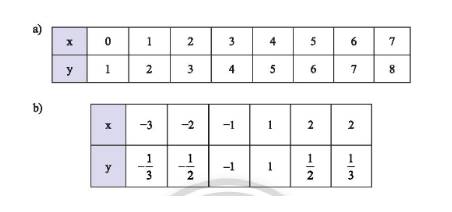
Thảo luận (1)Hướng dẫn giảia) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).
(Trả lời bởi Hà Quang Minh)
Cho hàm số \(y = f\left( x \right) = 3x\)
a) Tính \(f\left( 1 \right);f\left( { - 2} \right);f\left( {\dfrac{1}{3}} \right)\).
b) Lập bảng các giá trị tương ứng của \(y\) khi \(x\) lần lượt nhận các giá trị:
\( - 3; - 2; - 1;0;1;2;3\).
Thảo luận (1)Hướng dẫn giảia) \(f\left( 1 \right) = 3.1 = 3;f\left( { - 2} \right) = 3.\left( { - 2} \right) = - 6;f\left( {\dfrac{1}{3}} \right) = 3.\dfrac{1}{3} = 1\).
b) Ta có: \(f\left( { - 3} \right) = 3.\left( { - 3} \right) = - 9;f\left( { - 1} \right) = 3.\left( { - 1} \right) = - 3\)
\(f\left( 0 \right) = 3.0 = 0;f\left( 2 \right) = 3.2 = 6;f\left( 3 \right) = 3.3 = 9\);
Ta lập được bảng sau
(Trả lời bởi Hà Quang Minh)
\(x\)
–3
–2
–1
0
1
2
3
\(y\)
–9
-6
–3
0
3
6
9
Cho hàm số \(y = f\left( x \right) = {x^2} + 4\). Tính \(f\left( { - 3} \right);f\left( { - 2} \right);f\left( { - 1} \right);f\left( 0 \right);f\left( 1 \right)\)
Thảo luận (1)Hướng dẫn giải\(f\left( { - 3} \right) = {\left( { - 3} \right)^2} + 4 = 9 + 4 = 13\);
\(f\left( { - 2} \right) = {\left( { - 2} \right)^2} + 4 = 4 + 4 = 8\);
\(f\left( { - 1} \right) = {\left( { - 1} \right)^2} + 4 = 1 + 4 = 5\);
\(f\left( 0 \right) = {0^2} + 4 = 0 + 4 = 4\);
\(f\left( 1 \right) = {1^2} + 4 = 1 + 4 = 5\).
(Trả lời bởi Hà Quang Minh)