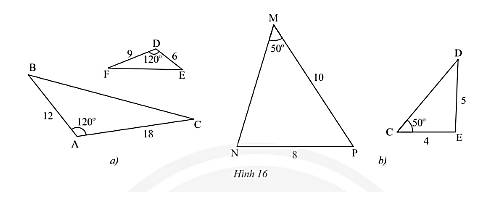
- Xét Hình 16a
Ta có: \(\frac{{DE}}{{AB}} = \frac{6}{{12}} = \frac{1}{2};\frac{{DF}}{{AC}} = \frac{9}{{18}} = \frac{1}{2}\)
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\frac{{DE}}{{AB}} = \frac{{DF}}{{AC}} = \frac{1}{2}\)
\(\widehat {BAC} = \widehat {EDF} = 120^\circ \)
Do đó, \(\Delta DEF\backsim\Delta ABC\) (c.g.g)
- Xét Hình 16b
Ta có: \(\frac{{CE}}{{NP}} = \frac{4}{8} = \frac{1}{2};\frac{{DE}}{{MP}} = \frac{5}{{10}} = \frac{1}{2}\)
Tuy nhiên, quan sát hình vẽ ta có thể thấy góc tạo bởi cạnh \(MP;NP\) là \(\widehat P\) và góc tạo bởi cạnh \(DE;CE\) là góc \(\widehat E\).
Ta thấy hai góc này không bằng nhau nên chúng không đồng dạng.